F(x) là một nguyên hàm của hàm số f(x) => F'(x) = f(x)
Đồng nhất ta được 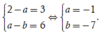
Chọn B.
F(x) là một nguyên hàm của hàm số f(x) => F'(x) = f(x)
Đồng nhất ta được 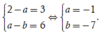
Chọn B.
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
Cho hai hàm số F x = x 2 + a x + b e - x và f x = - x 2 + 3 x + 6 e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x).
A. a = 1,b = -7
B. a = -1,b = -7
C. a = -1,b = 7
D. a = 1,b = 7
Cho hai hàm số F x = x 2 + a x + b e - x và f x = - x 2 + 3 x + 6 e - x Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a= -1;b=7.
B. a=1;b=7.
C. a=1;b= -7.
D. a= -1;b= -7.
Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox hoành tại ba điểm có hoành độ -2<a<b như hình vẽ. Biết rằng f(-2)+f(1)=f(a)+f(b). Để hàm số y = f ( x + m ) có 7 điểm cực trị thì mệnh đề nào dưới đây là đúng
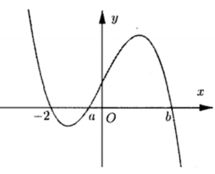
A. f(a)>0>f(-2)
B. f(-2)>0>f(a)
C. f(b)>0>f(a)
D. f(b)>0>f(-2)
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-1=2F(b). Tính I = ∫ a b f ( x ) d x
A. I=-1
B. I=1
C. I = - 1 2
D. I = 1 2
Biết F (x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F(3) = a + b 5 , trong đó a , b là các số nguyên. Tính tổng bình phương của a và b.
A. 121
B. 73
C. 265
D. 361
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3