Tam giác DIE vuông tại I có IK là trung tuyến thuộc cạnh huyền DE nên: KI = KD = (1/2).ED (tính chất tam giác vuông)
Suy ra tam giác IKD cân tại K
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Chứng minh rằng tứ giác BDCE là hình thoi
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Gọi I là giao điểm của EC và đường tròn (O’). Chứng minh rằng ba điểm D, A, I thẳng hàng
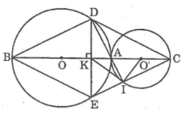
Cho hai đường tròn (O;R) và (O';R') tiếp xúc ngoài tại A (R> R').Vẽ các đường kính AOB ,AO'C .Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC .
a/ Chứng minh rằng tứ giác BDCE là hình thoi
b/ Gọi I là giao điểm của EC và đường tòn (O').Chứng minh rằng 3 điểm D,A,I thẳng hàng
c/Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
Bài 2: Hai đường tròn (O; R) và ( O' ;R^ , ) sao cho R >R^ , tiếp xúc ngoài tại C. Gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và đường tròn (O’). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Gọi giao điểm thứ 2 của đường thẳng DC với dường tròn (O’) là F.
a) Tứ giác AEBD là hình gì?
b) Chứng minh B, F, D thẳng hàng; Chứng minh MDBF nội tiếp
c) DB cắt đường (O’) tại G. Chứng minh DF, EG và AB đồng quy.
d) Chứng minh MF = 1/2 * DE tuyến của đường tròn (O’) và MF là tiếp tuyến của đường tròn (O')
Cho hai đường tròn (O;R) và (O;R') tiếp xúc ngoài tại A. vẽ tiếp tuyến chung ngoài BC . Gọi D là giao điểm của đường thẳng AC và đường tròn (O) . vẽ tiếp tuyến DE của (O') chứng minh BD=DE
Cho (O;R). Từ điểm A nằm ngoài (O;R), vẽ hai tiếp tuyến AM và AN với đường tròn (M và N là các tiếp điểm)
a) Chứng minh tam giác AMN cân
b) Vẽ đường kính MB của đường tròn (O;R). Chứng minh rằng OA//NB
c) Vẽ dây NC của (O;R) vuông góc với MB tại H. Gọi I là giao điểm Của AB và NH. Tính tỉ số NI/NC
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B ∈ (O), C ∈ (O'). Đường vuông góc với OO' kẻ từ A cắt BC ở M
a, Tính MA theo R và r
b, Tính diện tích tứ giác BCO'O theo R và r
c, Tính diện tích ∆BAC theo R và r
d, Gọi I là trung điểm của OO'. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM)
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn (D ∈ (O), E ∈ (O’)). Gọi M là giao điểm của BD và CE. Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn.
Cho hai đường tròn (O) và (O') có bán kính R và R' (R>R') tiếp xúc ngoài nhau tại C. gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và đường tròn (O') . DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. đƯờng thẳng DC cắt đường tròn (O') tại C và I.
a)Tứ giác AEBD là hình gì? VÌ Sao?
b)Chứng minh ba điểm E,I,B thẳng hàng.
C) đường thẳng DB cắt đường tròn (O') tại B và K . Chứng minh DI, EK và AB Đồng quy
