Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
Hướng dẫn làm bài:
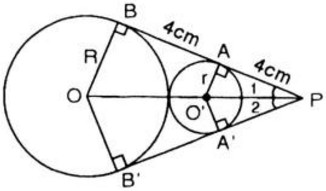
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)

Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
chung
Vậy ΔOBP ~ ∆ O’AP
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)











