Question

cho hai đường thằng xy vắt mn tại o. a) vẽ oz tia phân giác góc xom. b) vẽ ot ta phân giác góc yon. c) lấy a thuộc oz, b thuộc ot chứng minh a,o,b thẳng hàng 

Answer 1

a,b:

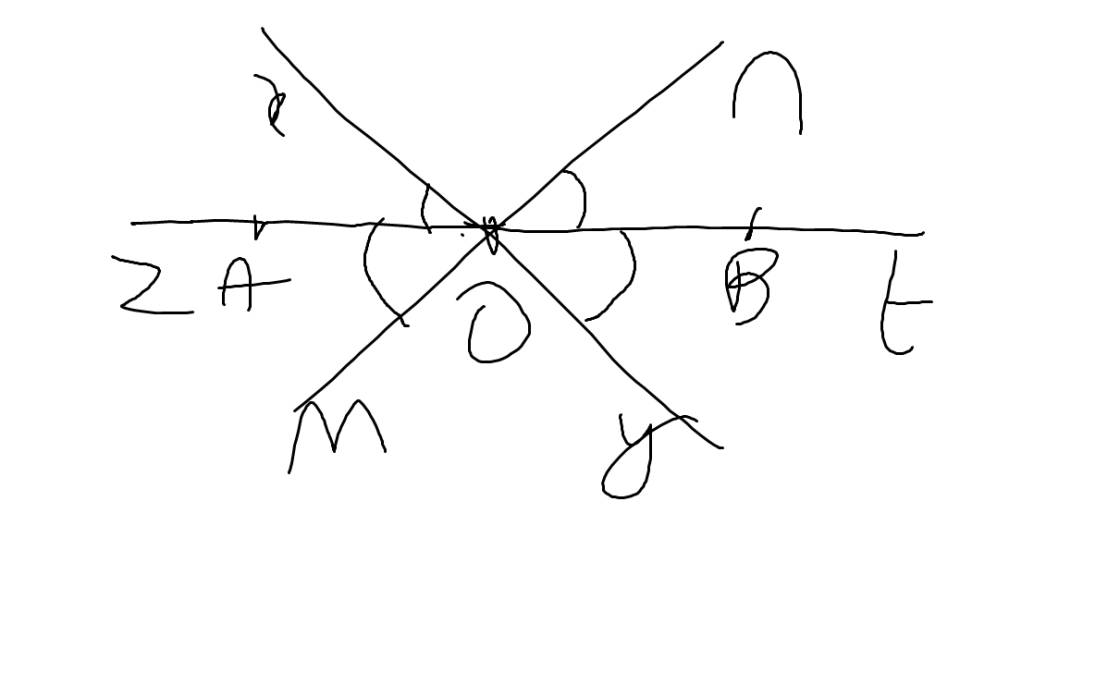
c: Ta có: \(\widehat{xOm}=\widehat{yOn}\)(hai góc đối đỉnh)

\(\widehat{xOz}=\widehat{mOz}=\dfrac{\widehat{xOm}}{2}\)(Oz là phân giác của góc xOm)

\(\widehat{tOn}=\widehat{tOy}=\dfrac{\widehat{nOy}}{2}\)(Ot là phân giác của góc nOy)

Do đó: \(\widehat{xOz}=\widehat{mOz}=\widehat{tOn}=\widehat{tOy}\)

=>\(\widehat{xOz}=\widehat{tOy}\)

mà \(\widehat{xOz}+\widehat{zOy}=180^0\)(hai góc kề bù)

nên \(\widehat{tOy}+\widehat{zOy}=180^0\)

=>\(\widehat{tOz}=180^0\)

=>\(\widehat{AOB}=180^0\)

=>A,O,B thẳng hàng