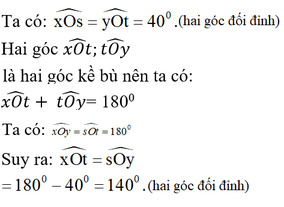Các câu hỏi tương tự
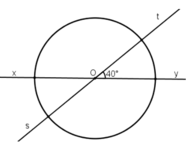
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40 ° . Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc A M B = 35 o .
Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.
cho hai đường tròn tâm (O) ,(O') cắt nhau tại A và B .đường phân giác của góc OBO' cắt các đường tròn (O) ,(O') tương ứng tại C,D.Hãy so sánh các góc ở tâm BOC và BO'D
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
Cho tam giác ABC có ba góc nhọn ( AB bé hơn AC ) nội tiếp trong đường tròn tâm O. Hai đường cao BE và CF của tam giác ABC cắt nhau tại H.a) chứng minh các tứ giác AEHF, BFEC nội tiếp được đường trònb) tia AH cắt BC tại D, kẻ đường kính AK của đường tròn tâm O. Chứng ming AB.AC AD.2Rc) đường thẳng EF cắt đường tròn tâm O tại hai điểm M và N ( M thuộc cung nhỏ AB ). Chứng minh AM ANd) vẽ đường tròn tâm i đường kính AH cắt đường tròn tâm O tại S ( S khác A ), đường thẳng SA và BC cắt nhau tại T. C...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn ( AB bé hơn AC ) nội tiếp trong đường tròn tâm O. Hai đường cao BE và CF của tam giác ABC cắt nhau tại H.
a) chứng minh các tứ giác AEHF, BFEC nội tiếp được đường tròn
b) tia AH cắt BC tại D, kẻ đường kính AK của đường tròn tâm O. Chứng ming AB.AC= AD.2R
c) đường thẳng EF cắt đường tròn tâm O tại hai điểm M và N ( M thuộc cung nhỏ AB ). Chứng minh AM = AN
d) vẽ đường tròn tâm i đường kính AH cắt đường tròn tâm O tại S ( S khác A ), đường thẳng SA và BC cắt nhau tại T. Chứng minh ba điểm T, M, N thẳng hàng
cho△ABC có ba góc nhọn nội tiếp đường tròn tâm O , bán kính R. Hạ các đường cao AH,BK của tam giác . các tia AH,BK lần lượt cắt (O) tại các điểm thứ hai là D;E.
a)Chứng minh tứ giác AKHB nội tiếp một đường tròn. Xác định tâm của đường tròn đó
b)chứng minh rằng :HK song song với DE
Cho đường tròn tâm O có hai đường kính AB và CD vuông góc với nhau. Lấy M cung nhỏ AC, vẽ tiếp tuyến với đường tròn tâm O tại M cắt đường thẳng CD tại S. CM góc MSD = 2lần góc MBA
Cho đường tròn ( O,R) tia tiếp tuyến Ax, trên Ax lấy điểm M sao cho OM = 2R, Om cắt đường tròn O tại N
a) tính AM theo R
b) tính số đo góc ở tâm tạo bởi OA và ON
c) tính số đo cung nhỏ, cung lớn AN
Cho tam giác ABC vuông tại A, có AB14, BC50. Đường Phân Giác của góc ABC và đưởng trung trực của cạnh AC cắt nhau tại E.1. Chứng Minh tứ giác ABCE nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn này.2. Tính BE.3. Vẽ đường kính EF của đường tròn tâm (O). AE và BF cắt nhau tại P. Chứng Minh các đường thẳng BE,PO,AF đồng quy.4. Tính diện tích phấn hình tròn (O) nằm ngoài ngũ giác ABFCE.
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB=14, BC=50. Đường Phân Giác của góc ABC và đưởng trung trực của cạnh AC cắt nhau tại E.
1. Chứng Minh tứ giác ABCE nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn này.
2. Tính BE.
3. Vẽ đường kính EF của đường tròn tâm (O). AE và BF cắt nhau tại P. Chứng Minh các đường thẳng BE,PO,AF đồng quy.
4. Tính diện tích phấn hình tròn (O) nằm ngoài ngũ giác ABFCE.