Các câu hỏi tương tự
Cho hàm số y f(x) liên tục trên đoạn [ a;b ] và thỏa mãn điều kiện f(x) f( a + b - x )
∀
x
∈
a
;
b
. Hỏi mệnh đề nào sau đây đúng? A.
∫
a
b
x
f
x
d
x
-
a
+
b
∫
a
b...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [ a;b ] và thỏa mãn điều kiện f(x) = f( a + b - x ) ∀ x ∈ a ; b . Hỏi mệnh đề nào sau đây đúng?
A. ∫ a b x f x d x = - a + b ∫ a b f x d x
B. ∫ a b x f x d x = a + b ∫ a b f x d x
C. ∫ a b x f x d x = - a + b 2 ∫ a b f x d x
D. ∫ a b x f x d x = a + b 2 ∫ a b f x d x
Cho hàm số y f(x) liên tục trên [a;b]. Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
α
;
β
]
∀
x
∈
[
a
;
b
]
hơn nữa f(u) liên...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ α ; β ] ∀ x ∈ [ a ; b ] hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A. ∫ a b f ( u ( x ) ) u ' d x = ∫ u ( a ) u ( b ) f ( u ) d u
B. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
C. ∫ u ( a ) u ( b ) f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
D. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( x ) d x
Cho hàm số y f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x c (acb) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng x a; x b. Mệnh đề nào dưới đây đúng ? A.
S
∫
a
c
f
(
x...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x = c (a<c<b) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x = a; x = b. Mệnh đề nào dưới đây đúng ?
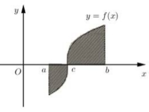
A. S = ∫ a c f ( x ) d x - ∫ c b f ( x ) d x
B. S = - ∫ a c f ( x ) d x + ∫ c b f ( x ) d x
C. S = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x
D. S = ∫ a b f ( x ) d x
Cho hàm số
y
f
(
x
)
liên tục trên đoạn [a;b] có đồ thị như hình bên và
c
∈
a
;
b
. Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số
y
f
(
x
)
và các đường thẳng
y
0
,
x
a...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b] có đồ thị như hình bên và c ∈ a ; b . Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số y = f ( x ) và các đường thẳng y = 0 , x = a , x = b . . Mệnh đề nào sau đây sai?
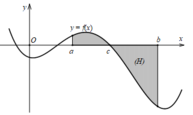
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a c f x d x − ∫ c b f x d x
C. S = ∫ a b f x d x
D. S = ∫ a c f x d x + ∫ b c f x d x
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số yf(x) liên tục, có đạo hàm trên đoạn [a;b] và đồ thị hàm số f (x) trên [a;b] là đường cong như hình vẽ. Khi đó, mệnh đề nào sau đây đúng? A.
min
x
∈
a
:
b
f
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục, có đạo hàm trên đoạn [a;b] và đồ thị hàm số f' (x) trên [a;b] là đường cong như hình vẽ. Khi đó, mệnh đề nào sau đây đúng?
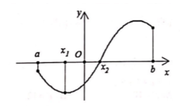
A. min x ∈ a : b f x = f b
B. min x ∈ a : b f x = f x 1
C. min x ∈ a : b f x = f a
D. min x ∈ a : b f x = f x 2
Cho các mệnh đề :1) Hàm số yf(x) có đạo hàm tại điểm
x
0
thì nó liến tục tại
x
0
. 2) Hàm số yf(x) liên tục tại
x
0
thì nó có đạo hàm tại điểm
x
0
.3) Hàm số yf(x) liên tục trên đoạn [a;b] và f(a).f(b)0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).4) Hàm số yf(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị n...
Đọc tiếp
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số yf(x) liên tục trên đoạn
a
;
b
và f(x)0
∀
x
∈
a
;
b
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số yf(x), trục hoành và 2 đường thẳng xa, xb (ab). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x