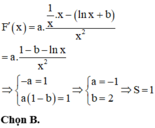Các câu hỏi tương tự
Tìm nguyên hàm của hàm số
f
(
x
)
2008
+
ln
2
x
x
có dạng
F
(
x
)
a
ln
x
+
ln
x
3
b
+
C
. Khi đó tổng S a + b là? A. 2012 B. 2010 C. 2009 D. 2011
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011
Cho
F
x
a
x
ln
x
+
b
là một nguyên hàm của hàm số
f
x
1
+
ln
x
x
2
trong đó
a
,
b
∈
ℤ...
Đọc tiếp
Cho F x = a x ln x + b là một nguyên hàm của hàm số f x = 1 + ln x x 2 trong đó a , b ∈ ℤ . Tính S = a + b
A. S = -2
B. S = 1
C. S = 2
D. S = 0
Cho F(x) là một nguyên hàm của hàm số
1
e
x
+
1
, thỏa mãn
F
(
0
)
-
ln
2
. Tìm tập nghiệm S của phương trình
F
(
x
)
+
l
n
(
e
x
+
1
)
3
A. ...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F ( 0 ) = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + l n ( e x + 1 ) = 3
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Cho F(x)
a
x
(lnx+b) là một nguyên hàm của hàm số
f
(
x
)
1
+
ln
x
x
2
trong đó a,b
∈
Z. Tính S a+b A. S -2 B. S 1...
Đọc tiếp
Cho F(x) = a x (lnx+b) là một nguyên hàm của hàm số f ( x ) = 1 + ln x x 2 trong đó a,b ∈ Z. Tính S = a+b
A. S = -2
B. S = 1
C. S = 2
D. S = 0
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
Kí hiệu F (x) là một nguyên hàm của hàm số
f
(
x
)
1
e
x
+
1
, biết
F
0
-
ln
2
. Tìm tập nghiệm S của phương trình
F
(
x
)
+
ln
(
e
x
+
1
)
3
. A.
S
-...
Đọc tiếp
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Cho hàm số
f
(
x
)
l
n
(
x
2
-
3
x
)
. Tập nghiệm S của phương trình f(x) 0 là: A. S
∅
B. S
3
2
C. S {0;3} D. S
-
∞
;
0
∪
3...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 3 x ) . Tập nghiệm S của phương trình f'(x) = 0 là:
A. S = ∅
B. S = 3 2
C. S = {0;3}
D. S = - ∞ ; 0 ∪ 3 ; + ∞
Cho hàm số f(x) xác định và có đạo hàm f(x) liên tục trên đoạn
1
;
3
,
f
x
≠
0
với mọi
x
∈
1
;
3
, đồng thời
f
x
1
+
f
x...
Đọc tiếp
Cho hàm số f(x) xác định và có đạo hàm f'(x) liên tục trên đoạn 1 ; 3 , f x ≠ 0 với mọi x ∈ 1 ; 3 , đồng thời f ' x 1 + f x 2 = f x 2 x − 1 2 v à f 1 = − 1 . Biết rằng ∫ 1 3 f x d x = a ln 3 + b a , b ∈ ℤ , tính tổng S = a + b 2 .
A. S = 2
B. S = 0
C. S = 4
D. S = -1
F(x) là nguyên hàm của hàm số
f
x
x
3
+
x
thỏa .
F
1
0
,
F
x
x
4
a
+
x
2
b
-
3
c
Tính S a + b + c ? A. 10 B. 12 C. 14 D. 16
Đọc tiếp
F(x) là nguyên hàm của hàm số f x = x 3 + x thỏa . F 1 = 0 , F x = x 4 a + x 2 b - 3 c Tính S = a + b + c ?
A. 10
B. 12
C. 14
D. 16