Các câu hỏi tương tự
Cho hàm số y f(x) thoả mãn điều kiện f(1) 12, f’(x) liên tục trên
ℝ
và
∫
1
4
f
x
d
x
17
. Khi đó f(4) bằng A. 5 B. 29 C. 19 D. 9
Đọc tiếp
Cho hàm số y = f(x) thoả mãn điều kiện f(1) = 12, f’(x) liên tục trên ℝ và ∫ 1 4 f ' x d x = 17 . Khi đó f(4) bằng
A. 5
B. 29
C. 19
D. 9
Cho A ( 1; 4; 2); B ( -1; 2;4) và
d
:
x
-
1
-
1
y
+
2
1
z
2
. Điểm M di động trên (d), khi đó GTNN của
F
M
A
2
+
M...
Đọc tiếp
Cho A ( 1; 4; 2); B ( -1; 2;4) và d : x - 1 - 1 = y + 2 1 = z 2 . Điểm M di động trên (d), khi đó GTNN của F = M A 2 + M B 2 bằng bao nhiêu?
![]()
![]()
![]()
![]()
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có bảng biến thiên như sau Khi đó
f
x
m
có bốn nghiệm phân biệt
x
1
x
2
x...
Đọc tiếp
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có bảng biến thiên như sau
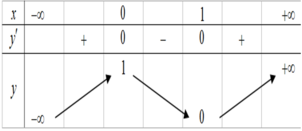
Khi đó f x = m có bốn nghiệm phân biệt x 1 < x 2 < x 3 < 1 / 2 < x 4 khi và chỉ khi
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) có đạo hàm liên tục trên R và đồ thị hàm số y f(x) như hình vẽ. Bất phương trình
f
(
x
)
≤
3
x
-
2
x
+
m
có nghiệm trên
(
-
∞
;
1
]
khi và chỉ khi
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R và đồ thị hàm số y = f'(x) như hình vẽ. Bất phương trình f ( x ) ≤ 3 x - 2 x + m có nghiệm trên ( - ∞ ; 1 ] khi và chỉ khi
![]()
![]()
![]()
![]()
Cho hàm số y f(x ) ax3+ bx2+ cx+ d có bảng biến thiên như sau: Khi đó |f(x)| m có 4 nghiệm phân biệt
x
1
x
2
x
3
1
2
x
4
khi và chỉ khi A. ½ m 1 B. 0 m C. m 1 D. m 1/2
Đọc tiếp
Cho hàm số y= f(x )= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
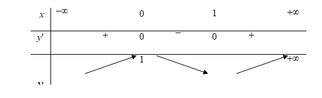
Khi đó |f(x)| = m có 4 nghiệm phân biệt x 1 < x 2 < x 3 < 1 2 < x 4 khi và chỉ khi
A. ½< m< 1
B. 0< m
C. m> 1
D. m< 1/2
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x - 3 ) 2 . Khi đó số cực trị của hàm số y = f ( 2 x + 1 ) là
A. 0
B. 2
C. 1
D. 3
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số y f(x) Hàm số y f’(x) có bảng biến thiên như sau Bất phương trình
f
(
x
)
3
e
x
+
2
+
m
có nghiệm
x
∈
(
-
2
;
2
)
khi và chỉ khi A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x) Hàm số y= f’(x) có bảng biến thiên như sau
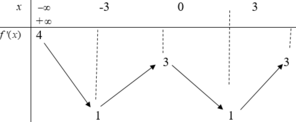
Bất phương trình f ( x ) < 3 e x + 2 + m có nghiệm x ∈ ( - 2 ; 2 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho (S):
x
-
1
2
+
y
+
2
2
+
z
-
3
2
4 và A(2; -1; 2); B(1; 0; 4). Khi đó: A. (S) và đường thẳng AB tiếp xúc. B. Đường...
Đọc tiếp
Cho (S): x - 1 2 + y + 2 2 + z - 3 2 = 4 và A(2; -1; 2); B(1; 0; 4). Khi đó:
A. (S) và đường thẳng AB tiếp xúc.
B. Đường thẳng AB đi qua tâm (S).
C. Đường thẳng AB không cắt (S).
D. Đoạn AB và (S) có đúng 1 điểm chung




