Các câu hỏi tương tự
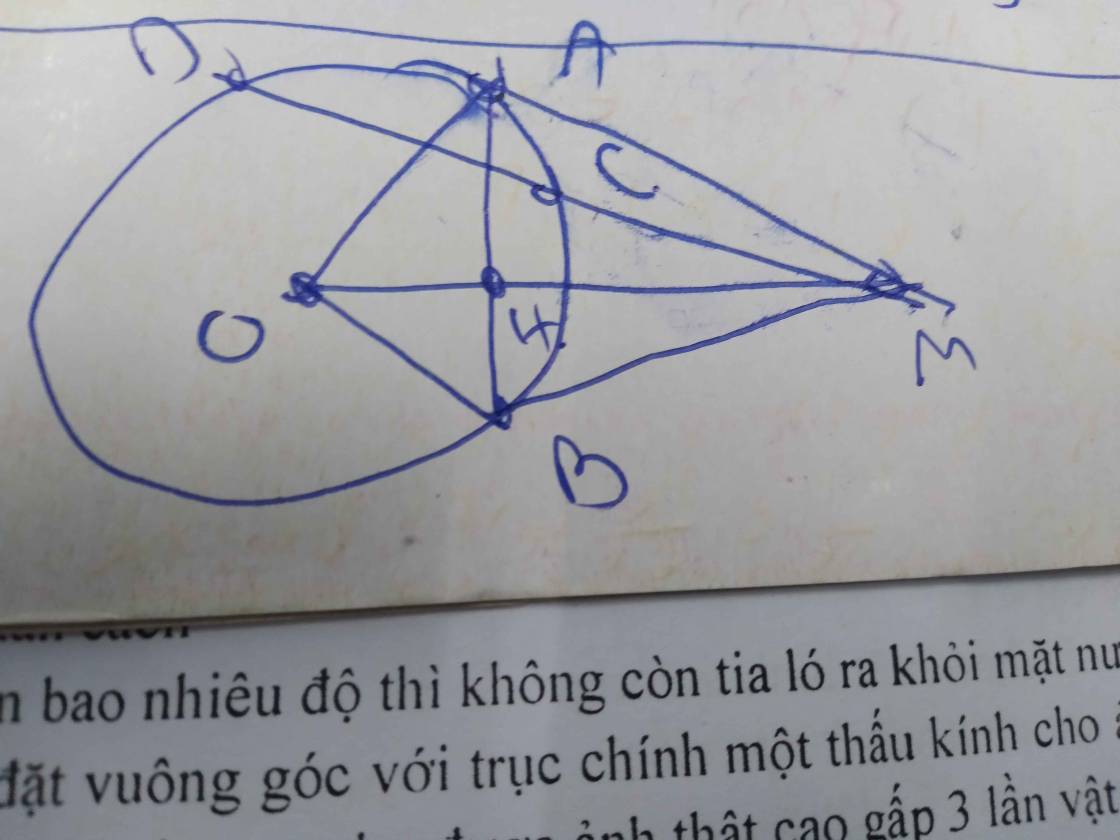
Từ điểm M nằm bên ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA,MB đến đường tròn (O) ( AB là các tiếp điểm và C nằm giữa M, D)a) C/m MA bình MC.MDb) Gọi I là trung điểm của CD. C/m 5 điểm M, A, O, I, B cùng nằm trên một đường tròn.c) Gọi H là giao điểm của AB và MO. C/m tứ giác CHOD nội tiếp đường tròn d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). C/m A,B,K thẳng hàng.
Đọc tiếp
Từ điểm M nằm bên ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA,MB đến đường tròn (O) ( AB là các tiếp điểm và C nằm giữa M, D)
a) C/m MA bình= MC.MD
b) Gọi I là trung điểm của CD. C/m 5 điểm M, A, O, I, B cùng nằm trên một đường tròn.
c) Gọi H là giao điểm của AB và MO. C/m tứ giác CHOD nội tiếp đường tròn
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). C/m A,B,K thẳng hàng.
Bài 1:Từ điểm M nằm ngoài đường tròn (O). Vẽ các tiếp tuyến AM,BM với đường tròn (A,B là các tiếp điểm) và cát tuyến MCD không đi qua tâm O (C nằm giữa M và D) với đường tròn(O).
a)C/m: Tứ giác MAOB nội tiếp
b)C/m: MA2=MC.MD
c)Đường thẳng MO cắt AB tại H và cắt (O) tại I và K( I nằm giữa M và K).C/m: CK là tia phân giác của góc DCH
Từ một điểm M bên ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O), ở đây A, B là các tiếp điểm và C nằm giữa M, D.a) Chứng minh MA2 MC.MD ;b) Gọi I là trung điểm của CD. Chứng minh rằng 5 điểm M, A, O, I, B cùng nằm trên một đường tròn ;c) Gọi H là giao điểm của AB và MO. Chứng minh tứ giác CHOD nội tiếp được đường tròn. Suy ra AB là đường phân giác của góc CHD ;d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng min...
Đọc tiếp
Từ một điểm M bên ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O), ở đây A, B là các tiếp điểm và C nằm giữa M, D.
a) Chứng minh MA2 = MC.MD ;
b) Gọi I là trung điểm của CD. Chứng minh rằng 5 điểm M, A, O, I, B cùng nằm trên một đường tròn ;
c) Gọi H là giao điểm của AB và MO. Chứng minh tứ giác CHOD nội tiếp được đường tròn. Suy ra AB là đường phân giác của góc CHD ;
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh A, B, K thẳng hàng.
Cho điểm M nằm ngoài đường tròn (O).vẽ các tiếp tuyến MA,MB(A,B là các tiếp điểm) và cát tuyến MCD ko đi qua O (C nằm giữa M và D) với đường tròn (O). Đoạn thẳng MO cắt AB và (O) theo thứ tự tại H và I. chứng minh rằng:
a) Tứ giác MAOB nội tiếp đường tròn
b) MC.MD=MA2
c) OH.OM+MC.MD=MO2
d) CI là phân giác của góc MCH
Cho điểm M nằm ngoài đường tròn tâm O. Vẽ tiếp tuyếp MA, MB với đường tròn. Vẽ cát tuyến MCD không đi qua tâm O, OM cắt AB và (O) lần lượt tại H và I. Chứng minh
a) tứ giác MAOB nội tiếp
b) MC.MD=MA^2
c) OH.OM+MC.MD=MO^2
Cho đường tròn tâm O bán kính R và điểm M nằm ngoài đường tròn. Từ M vẽ hai tiếp tuyến MA, MB với đường tròn (A,B là hai tiếp tuyến)
a) Chứng minh tứ giác MAOB là nội tiếp trong một đường tròn
b) Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Chứng minh hệ thức MA^2 MC.MD
c) Gọi H là trung điểm của dây CD. Chứng minh HM là tia phân giác của góc AHB
giúp em với ạ em đang cần gấp
Đọc tiếp
Cho đường tròn tâm O bán kính R và điểm M nằm ngoài đường tròn. Từ M vẽ hai tiếp tuyến MA, MB với đường tròn (A,B là hai tiếp tuyến) a) Chứng minh tứ giác MAOB là nội tiếp trong một đường tròn b) Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Chứng minh hệ thức MA^2 = MC.MD c) Gọi H là trung điểm của dây CD. Chứng minh HM là tia phân giác của góc AHB giúp em với ạ em đang cần gấp
Từ điểm M nằm ngoài đường tròn O . Vẽ tiếp tuyến MA,MB với đường tròn ( A,B là các tiếp điểm ) và cát tuyến MCD không đi qua O ( C nằm giẵ M và D ) với đường tròn O
a) C/m tứ giác MAOB nội tiếp
b)C/m MA2 =MC.MD
c) Đường thẳng MO cắt AB tại H và cắt O tại I và K ( I nằm giữa M và K ) . C/m CK là phân giác của DCH
Cho điểm M nằm ngoài đường tròn (O;R). Qua M vẽ hai tiếp tuyến MA, MB và cát tuyến MCD (A,B,C,D thuộc đường tròn tâm O), tia MC nằm giữa hai tia MO và MA. Gọi H là giao điểm của AB và MO.a/ CM tứ giác MAOB nội tiếp.b/ Gọi K là trung điểm CD. Chứng minh 5 điểm M, A, K, O, B cùng thuộc một đường tròn. Từ đó suy ra KM là phân giác của góc AKB.c/ Đường thẳng OK cắt đường thẳng AB tại N. Chứng minh ND là tiếp tuyến đường tròn (O)
Đọc tiếp
Cho điểm M nằm ngoài đường tròn (O;R). Qua M vẽ hai tiếp tuyến MA, MB và cát tuyến MCD (A,B,C,D thuộc đường tròn tâm O), tia MC nằm giữa hai tia MO và MA. Gọi H là giao điểm của AB và MO.
a/ CM tứ giác MAOB nội tiếp.
b/ Gọi K là trung điểm CD. Chứng minh 5 điểm M, A, K, O, B cùng thuộc một đường tròn. Từ đó suy ra KM là phân giác của góc AKB.
c/ Đường thẳng OK cắt đường thẳng AB tại N. Chứng minh ND là tiếp tuyến đường tròn (O)
Đề thi tuyển sinh lớp 10 Bình Phước năm 2018Câu 5 :(2 ,5 điểm) Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB(A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O(C nằm giữa M và D; O và B nằm hai phía so với cát tuyến MCD).a) Chứng minh: Tứ giác MAOB nội tiếpb) Chứng minh: MB^2MC.MDc) Gọi H là giao điểm của AB và OM.Chứng minh: AB là phân giác của widehat{CHD}
Đọc tiếp
Đề thi tuyển sinh lớp 10 Bình Phước năm 2018
Câu 5 :(2 ,5 điểm)
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB(A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O(C nằm giữa M và D; O và B nằm hai phía so với cát tuyến MCD).
a) Chứng minh: Tứ giác MAOB nội tiếp
b) Chứng minh: \(MB^2=MC.MD\)
c) Gọi H là giao điểm của AB và OM.Chứng minh: AB là phân giác của \(\widehat{CHD}\)