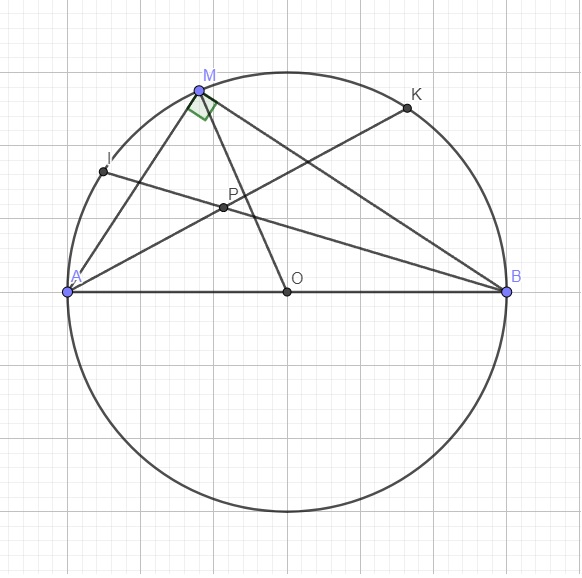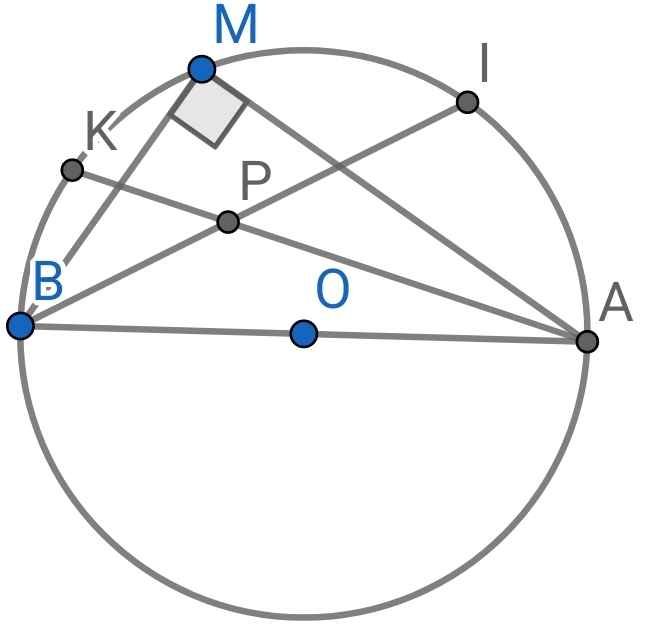
a) Do MA ⊥ MB (gt)
⇒ ∠MAB = 90⁰
⇒ M, A, B thuộc đường tròn đường kính AB
Mà M, A, B thuộc (O)
⇒ O là trung điểm của AB
⇒ A, O, B thẳng hàng
b) Do I là điểm chính giữa của cung nhỏ MA (gt)
⇒ sđ cung AI = sđ cung MI
⇒ ∠ABI = ∠MBI (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ BI là tia phân giác của ∠ABM
Do K là điểm chính giữa của cung MB (gt)
⇒ sđ cung BK = sđ cung MK
⇒ ∠BAK = ∠MAK (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ AK là tia phân giác của ∠BAM
Mà P là giao điểm của AK và BI (gt)
⇒ P là giao điểm của ba đường phân giác của ∆MAB
⇒ P là tâm đường tròn nội tiếp ∆MAB
a.
Do \(OM=OA=R\Rightarrow\Delta OAM\) cân tại O
\(\Rightarrow\widehat{OAM}=\widehat{OMA}\Rightarrow\widehat{AOM}=180^0-\left(\widehat{OAM}+\widehat{OMA}\right)=180^0-2\widehat{OMA}\)
Tương tự, \(\Delta OBM\) cân tại O
\(\Rightarrow\widehat{BOM}=180^0-2\widehat{OMB}\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2\left(\widehat{OMA}+\widehat{OMB}\right)\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2.\widehat{AMB}=360^0-2.90^0=180^0\)
\(\Rightarrow A,O,B\) thẳng hàng
b.
Do I là điểm chính giữa cung MA \(\Rightarrow sđ\stackrel\frown{AI}=sđ\stackrel\frown{MI}\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow BI\) là tia phân giác góc \(\widehat{ABM}\) (1)
Do K là điểm chính giữa cung MB \(\Rightarrow sđ\stackrel\frown{MK}=sđ\stackrel\frown{BK}\Rightarrow\widehat{MAK}=\widehat{BAK}\)
\(\Rightarrow AK\) là tia phân giác góc \(\widehat{MAB}\) (2)
(1);(2) \(\Rightarrow P\) là giao điểm 2 đường phân giác trong của tam giác MAB
\(\Rightarrow P\) là tâm đường tròn nội tiếp tam giác MAB