Theo giả thiết AMO = ANO = AIO = 90o = > 5 điểm A, O, M, N, I thuộc đường tròn đường kính AO 0,25
=> AIN = AMN, AIM = ANM (Góc nội tiếp cùng chắn một cung)
AM = AN => ∆AMN cân tại A => AMN = ANM
=> AIN = AIM => đpcm
Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Trên tia đối của tia BC lấy điểm A (A khác B). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn (O) (M và N là các tiếp điểm). Gọi I là trung điểm của BC.
2) Gọi K là giao điểm của MN và BC. Chứng minh 2 A K = 1 A B + 1 A C .
Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Trên tia đối của tia BC lấy điểm A (A khác B). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn (O) (M và N là các tiếp điểm). Gọi I là trung điểm của BC.
3) Đường thẳng qua M và vuông góc với đường thẳng ON cắt (O) tại điểm thứ hai là P. Xác định vị trí của điểm A trên tia đối của tia BC để AMPN là hình bình hành.
Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Trên tia đối của tia BC lấy điểm A ( A khác B ). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn (O) ( M và N là các tiếp điểm). Gọi I là trung điểm của BC.
a, Chứng minh A, O, M, N, I cùng thuộc một đường tròn
b, Gọi K là giao điểm của MN và BC. H là giao điểm của MN và AO. Chứng minh rằng AK. AI = AB. AC = AM^2
c, Chứng minh: \(\frac{2}{AC}=\frac{1}{AB}+\frac{1}{AC}\)
Cho đường tròn (O;R) và dây BC cố định. Trên tia đối của tia BC lấy điểm A. Kẻ các tiếp tuyến AM, AN với đường tròn (O) (M và N là các tiếp điểm, N thuộc cung BC nhỏ). Gọi H là trung điểm của dây BC. 1) Chứng minh bốn điểm A, M, 0, H cũng thuộc một đường tròn. 2) MN cắt OA tại điểm I. Chứng minh rằng AI. AO= AM²
Cho đường tròn (O) và một dây BC cố định không đi qua O. Trên tia đối của tia BC lấy một điểm A bất kì. Vẽ các tiếp tuyến AM, AN tới (O) (M, N là các tiếp điểm). MN cắt các đưòng AO và BC lần lượt ở H và K. Gọi I là trung điểm của BC
a, Chứng minh: AH.AO = AB.AC = M A 2
b, Chứng minh tứ giác BHOC nội tiếp
c, Vẽ dây MP song song với BC. Chứng minh N, I, P thẳng hàng
d, Khi A di động trên tia đôi của tia BC, chứng minh trọng tâm tam giác MBC chạy trên một đường tròn cố định
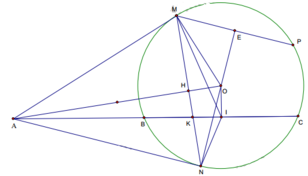
Cho ba điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua hai điểm C và B ( O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) ( M. N là hai tiếp điểm). Gọi I là trung điểm của BC.
1) Chứng minh bốn điểm O, I, A, M cùng thuộc một đường tròn.
2) Gọi E, H lần lượt là giao điểm của OA với đường tròn (O) và MN. Chứng minh BE là tia phân giác của góc ABH.
3) Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác OHI luôn nằm trên một đường thẳng cố định
): Cho đường tròn (O) và hai điểm A, B thuộc (O) sao cho đường thẳng AB không đi qua tâm O. Trên tia đối của tia AB lấy điểm M khác A, từ M kẻ hai tiếp tuyến ME, MF với đường tròn (O) (E, F là các tiếp điểm). Gọi H là trung điểm của dây AB. Các điểm K và I theo thứ tự là giao điểm của đường thẳng EF với các đường thẳng OM và OH.
1/ Chứng minh 5 điểm M, O, H, E, F cùng nằm trên một đường tròn.
2/ Chứng minh: OH.OI = OK. OM,
3) EF luôn đi qua một điểm cố định khi M thay đổi trên tia đối của tia AB
4/ Chứng minh: IA, IB là các tiếp điểm của đường tròn (O)
Cho đường tròn tâm O và đường thẳng d cắt đường tròn tâm O tại hai điểm B và C (d không đi qua O). Trên tia đối của tia BC lấy điểm A (A nằm ngoài đường tròn tâm O). Kẻ AM và AN là các tiếp tuyến với đường tròn tâm O tại M và N. Gọi I là trung điểm của BC, AO cắt MN tại H, và cắt đường tròn tại các điểm P và Q (P nằm giữa A và O), BC cắt MN tại K.
a) Chứng minh 4 điểm O, M, N, I nằm trên cùng một đường tròn và AK. AI=AM2
b) Gọi D là trung điểm HQ, từ H kẻ đường thẳng vuông góc với MD, cắt đường thẳng MP tại E. Chứng minh P là trung điểm của ME.
GIÚP MK VỚI QAQ
Cho 3 điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua 2 điểm cố định C và B (O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) (M,N là 2 tiếp điểm ). Gọi I là trung điểm của BC.
1, Chứng minh 4 điểm O,I,A,M cùng thuộc 1 đường tròn
2, Gọi E,H lần lượt là giao điểm của OA cới đường tròn (O) và MN. Chứng minh BE là phân giác của góc ABH
3,Chứng minh rằng tâm đường tròn ngoại tiếp tan giác OHI luôn nằm trên một đường thẳng cố định
