Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên 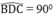
Suy ra : BD ⊥ AC (1)
Ta có : AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra : AD = DC

Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên 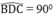
Suy ra : BD ⊥ AC (1)
Ta có : AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra : AD = DC
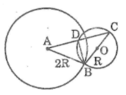
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O) .
a) Chứng minh rằng: OA vuông góc với BC và OA // BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC.
Chứng minh rằng: AE. AD = AH. AO
c,Gọi r là bán kính của đường tròn nội tiếp tam giac ABC. Tính độ dài đoạn thẳng BD theo Rvs r
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O) .
a) Chứng minh rằng: OA vuông góc với BC và OA // BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC.
Chứng minh rằng: AE. AD = AH. AO.
c) Chứng minh rằng: .góc AHE = góc OED
d) Gọi r là bán kính của đường tròn nội tiếp tam giác ABC. Tính độ dài đoạn thẳng BD theo R, r.
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O) .
a) Chứng minh rằng: OA vuông góc với BC và OA // BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC.
Chứng minh rằng: AE. AD = AH. AO.
c) Chứng minh rằng: .góc AHE = góc OED
d) Gọi r là bán kính của đường tròn nội tiếp tam giác ABC. Tính độ dài đoạn thẳng BD theo R, r.
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ hai tiếp tuyến |AB,AC với đường tròn (O) (B,C là các tiếp điểm). Vẽ dường kính CD của đường tròn (O). AD cắt đường tròn (O) tại N (N khác D), gọi H là giao điểm của OA và BC. Gọi M là giao điểm của AD và BC, E là giao điểm của OA và CN. Đường thẳng vuông góc với ME cắt EN,BC,DC lần lượt tại F,P,Q.Cmr: PF=PQ
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B,C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).
a) Chứng minh rằng: OA vuông góc với BC và OA song song với BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. CMR: AE.AD=AH.AO
c) CMR: Góc AHE bằng góc OED
d) Gọi r là bán kính của đường tròn nội tiếp tam giác ABC. Tính độ dài đoạn thẳng BD theo R và r.
Giải giúp mình câu d, còn những câu trên mình giải được rồi.
Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ các tiếp tuyến AB và AC đến (O) với B, C là tiếp điểm. Gọi H là giao điểm của BC với OA. Vẽ CD là đường kính của (O), AD cắt đường tròn (O) tại điểm thứ 2 là E. a) Chứng minh: ∆CED vuông tại E và OA vuông góc BC tại H b) Chứng minh AE. AD = AH. AO và AHE = ADO c) Gọi I là giao điểm của BC và DE. Chứng mình DHO = EHA và 1/AE + 1/AD = 2/AI
Từ điểm A nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB và AC với đường tròn (O;R) . Gọi H là giao điểm của AO và BC.
a) Chứng minh AO là đường trung trực BC
b) Vẽ đường kính CD của đường tròn (O) , AD cắt đường tròn (O) tại E. Chứng minh \(AB^2=AE.AD\)
c) Tiếp tuyến E của đường tròn (O) cắt AB , AC lần lượt tại M và N . Chứng minh chu vi \(\Delta ANM=AB+AC\)
d) MN cắt AO tại I , EO cắt BC tại P . Chứng minh \(AE//IP\)
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a. Chứng minh OA vuông góc với BC tại H.
b. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn(O) tại E (E khác D). Chứng minh: AE.AD = AC^2
c. Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh rằng FD là tiếp tuyến của đường tròn (O).
Cho điểm A nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai tiếp điểm), gọi H là giao điểm của OA và BC.
a) Chứng minh rằng: OA vuông góc BC
b) Gọi D, E là hai giao điểm của OA với đường tròn (O) (D nằm giữa O và A). Chứng minh rằng: OH.HA = HD.HE
c) Chứng minh rằng: 2DH.AB = DA.BC