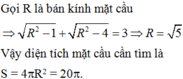Các câu hỏi tương tự
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng
r
2
2
. Mặt phẳng (P) chia khối trụ thành hai phần. Gọi
V
1
là thể tích của phần chứa tâm của đường tròn đáy và
V
2
thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số ...
Đọc tiếp
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng r 2 2 . Mặt phẳng (P) chia khối trụ thành hai phần. Gọi V 1 là thể tích của phần chứa tâm của đường tròn đáy và V 2 thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số V 1 V 2 .
A. V 1 V 2 = 3 π − 2 π − 2
B. V 1 V 2 = π − 2 3 π + 2
C. V 1 V 2 = 3 + 2 2
D. V 1 V 2 = 3 π + 2 π - 2
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng
r
2
2
. Mặt phẳng (P) chia khối trụ thành hai phần. Gọi
V
1
là thể tích của phần chứa tâm của đường tròn đáy và
V
2
thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số
V
1...
Đọc tiếp
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng r 2 2 . Mặt phẳng (P) chia khối trụ thành hai phần. Gọi V 1 là thể tích của phần chứa tâm của đường tròn đáy và V 2 thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số V 1 V 2 .
A. V 1 V 2 = 3 π − 2 π − 2
B. V 1 V 2 = π − 2 3 π + 2
C. V 1 V 2 = 3 + 2 2
D. V 1 V 2 = 3 π + 2 π − 2
Trong không gian với hệ tọa độ Oxyz, cho
A
1
;
2
;
-
3
,
B
3
2
;
3
2
;
-
1
2
,
C
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A 1 ; 2 ; - 3 , B 3 2 ; 3 2 ; - 1 2 , C 1 ; 1 ; 4 , D 5 ; 3 ; 0 , Gọi S 1 là mặt cầu tâm A bán kính bằng 3, S 2 là mặt cầu tâm B bán kính bằng 3 2 . Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S 1 , S 2 đồng thời song song với đường thẳng đi qua 2 điểm C D, .
A. 1
B. 2
C. 4
D. Vô số
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
2
;
-
3
,
B
3
2
;
3
2
;
-
1
2
,
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; - 3 , B 3 2 ; 3 2 ; - 1 2 , C 1 ; 1 ; 4 , D 5 ; 3 ; 0 . Gọi S 1 là mặt cầu tâm A bán kính bằng 3, S 2 là mặt cầu tâm B bán kính bằng 3 2 Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S 1 , S 2 đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 3
D. Vô số
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-30. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó. A.
21
. B.
2
6
. C. 6. D.
3
3
.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-3=0. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A. 21 .
B. 2 6 .
C. 6.
D. 3 3 .
Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là A.
5
4
πR
2
B.
πR
2
C.
7
4
πR
2
D.
3...
Đọc tiếp
Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là
A. 5 4 πR 2
B. πR 2
C. 7 4 πR 2
D. 3 2 πR 2
Cho mặt cầu tâm O, bán kính R=3. Mặt phẳng α cách tâm O của mặt cầu một khoảng bằng 1, cắt mặt cầu theo một đường tròn. Diện tích đường tròn bằng bao nhiêu
A. 4 π
B. 6 π
C. 8 π
D. 10 π
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
-
1
2
+
z
+
2
2
3
và hai đường thẳng...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y - 1 2 + z + 2 2 = 3 và hai đường thẳng d x : x - 2 1 = y 2 = z - 1 - 1 , ∆ : x 1 = y 1 = z - 1 - 1 Phương trình nào dưới đây là phương trình mặt phẳng cắt mặt cầu (S) theo giao tuyến là một đường tròn (C) có bán kính bằng 1 và song song với d và ∆ .
A. y+z+3=0
B. x+y+1=0
C. x+z-1=0
D. x+z+1=0
Cho A là điểm nằm trên mặt cầu (S) tâm (O), có bán kính R6cm. I, K là 2 điểm trên đoạn OA sao cho OIIKKA. Các mặt phẳng (α), (b) lần lượt qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo các đường tròn có bán kính
r
1
,
r
2
. Tính tỉ số
r
1
r
2
A.
r
1...
Đọc tiếp
Cho A là điểm nằm trên mặt cầu (S) tâm (O), có bán kính R=6cm. I, K là 2 điểm trên đoạn OA sao cho OI=IK=KA. Các mặt phẳng (α), (b) lần lượt qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo các đường tròn có bán kính r 1 , r 2 . Tính tỉ số r 1 r 2
A. r 1 r 2 = 4 10
B. r 1 r 2 = 5 3 10
C. r 1 r 2 = 3 10 4
D. r 1 r 2 = 3 10 5