Các câu hỏi tương tự
Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có AB2a,
B
C
2
3
a
. Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại
A
S
≠
A
. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tính...
Đọc tiếp
Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có AB=2a, B C = 2 3 a . Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại A S ≠ A . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tính bán kính R của mặt cầu đó.
![]()
![]()
![]()
![]()
Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có
A
B
2
a
,
B
C
2
3
a
. Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại
A
S
≠
A
. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tín...
Đọc tiếp
Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có A B = 2 a , B C = 2 3 a . Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại A S ≠ A . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tính bán kính R của mặt cầu đó.
A. R = 2 a
B. R = 3 a
C. R = 2 a
D. R = a
Trong mặt phẳng (P) cho đường tròn (C) có đường kính
A
B
2
. Trên đường thẳng vuông góc với (P) tại điểm A, lấy điểm S sao cho
S
A
5
. Xét điểm M thay đổi trên (C), mặt phẳng (α) qua A vuông góc với SB, lần lượt cắt SB, SM tại H và K. Diện tích tam giác AHK đạt giá trị lớn nhất bằng A.
5
9
B. 2 C.
4
5
D. 1
Đọc tiếp
Trong mặt phẳng (P) cho đường tròn (C) có đường kính A B = 2 . Trên đường thẳng vuông góc với (P) tại điểm A, lấy điểm S sao cho S A = 5 . Xét điểm M thay đổi trên (C), mặt phẳng (α) qua A vuông góc với SB, lần lượt cắt SB, SM tại H và K. Diện tích tam giác AHK đạt giá trị lớn nhất bằng
A. 5 9
B. 2
C. 4 5
D. 1
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1),
K
−
8
3
;
4
3
;
8
3
, O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phư...
Đọc tiếp
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1), K − 8 3 ; 4 3 ; 8 3 , O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phương trình là
A. d : x 1 = y − 6 − 2 = z − 6 2
B. d : x − 8 3 1 = y − 2 3 − 2 = z + 2 3 2
C. d : x + 4 9 1 = y − 17 9 − 2 = z − 19 9 2
D. d : x + 4 1 = y + 1 − 2 = z − 1 2
Trong không gian, cho các mệnh đề sau:I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).IV. Qua điểm A không thuộc mặt phẳng
(
α
)
, kẻ được đúng một đường thẳng song song với . Số mệnh đề đúng là A....
Đọc tiếp
Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).
IV. Qua điểm A không thuộc mặt phẳng ( α ) , kẻ được đúng một đường thẳng song song với .
Số mệnh đề đúng là
A. 2
B. 0
C. 1
D. 3
Trong không gian với hệ toạ độ Oxyz, cho tam giác nhọn ABC có H(2;2;1),K(
-
8
3
;
4
3
;
8
3
),O lần lượt là chân đường cao hạ từ các đỉnh A,B,C lên các cạnh BC,CA,AB. Đường thẳng qua A và vuông góc với mặt phẳng (ABC) là A.
x
+
4
1
y
+...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho tam giác nhọn ABC có H(2;2;1),K( - 8 3 ; 4 3 ; 8 3 ),O lần lượt là chân đường cao hạ từ các đỉnh A,B,C lên các cạnh BC,CA,AB. Đường thẳng qua A và vuông góc với mặt phẳng (ABC) là
A. x + 4 1 = y + 1 - 2 = z - 1 2
B. x + 4 9 1 = y - 17 9 - 2 = z - 19 9 2
C. x - 8 3 1 = y - 2 3 - 2 = z + 2 3 2
D. x 1 = y - 6 - 2 = z - 6 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-
2...
Đọc tiếp
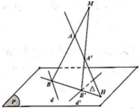
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
A. 8
B. 9
C. -9
D. 6
Cho hình lập phương a 1 có cạnh bằng a 1. Một đường thẳng d đi qua đỉnh D và tâm I cuả mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là: A. a 1 B. a
1
2
C.
a
2
5
D.
a...
Đọc tiếp
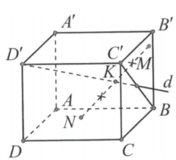
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3
Cho điểm P không thuộc đường thẳng a . Trên nửa mặt phẳng bờ a không chưa điểm P lấy hai điểm M và N không thuộc a sao cho M,N,P không thẳng hàng ,. Đoạn thẳng PN cắt a tại H.
a) Tia MH có nằm giữa MN và MP không ? Vì sao ?
b) Đoạn thẳng PM cắt a tại K . Đoạn thẳng MH có cắt đoạn thẳng NK không ? Vì sao ?




