Các câu hỏi tương tự
Cho hàm số yx3-12x-6 có đồ thị (C) và điểm A(m;0). Có bao nhiêu số nguyê
m
∈
-
5
;
5
để qua A ta kẻ được 3 tiếp tuyến tới đồ thị (C). A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Cho hàm số y=x3-12x-6 có đồ thị (C) và điểm A(m;0). Có bao nhiêu số nguyê m ∈ - 5 ; 5 để qua A ta kẻ được 3 tiếp tuyến tới đồ thị (C).
A. 1
B. 2
C. 3
D. 0
Cho hàm số yf(x) có đạo hàm liên tục trên tập R/
2
và có đồ thị hàm số yf’(x) như hình vẽ. Biết
f
1
≠
10
f(3)4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13 A. 2 B. 1 C. 0. D. 3
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
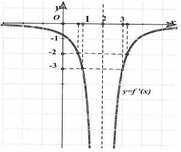
A. 2
B. 1
C. 0.
D. 3
Cho hàm số
y
x
3
-
3
x
+
2
có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y 9x-14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C). A. 4 điểm B. 2 điểm C. 1 điểm D. 3 điểm
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y = 9x-14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C).
A. 4 điểm
B. 2 điểm
C. 1 điểm
D. 3 điểm
Cho hàm số
y
x
3
−
3
x
+
2
có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y 9x - 14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C)? A. 4 điểm B. 2 điểm C. 1 điểm D. 3 điểm
Đọc tiếp
Cho hàm số y = x 3 − 3 x + 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y = 9x - 14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C)?
A. 4 điểm
B. 2 điểm
C. 1 điểm
D. 3 điểm
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số yf(x) xác định trên R. Đồ thị hàm số
y
f
(
x
)
cắt trục hoành tại 3 điểm a, b, c (
a
b
c
) như hình dưới: Biết f(b) 0 Đồ thị hàm số yf(x) cắt trục hoành tại bao nhiêu điểm phân biệt. A. 4 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
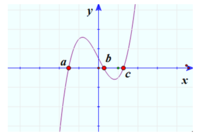
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
Cho hàm số yf(x) có đồ thị là (C), hàm số yf(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,bGiá trị
(
a
-
b
)
2
thuộc khoảng nào dưới đây A.
(
0
;
9
)
B.
(
12
;
16
)
C.
(
16...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
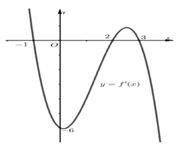
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng x=2 kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số y = x 3 - 3 x .
A. 7.
B. 3.
C. 9.
D. 8.
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng x = 2 kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số y = x 3 - 3 x .
A. 7.
B. 3.
C. 9.
D. 8.




