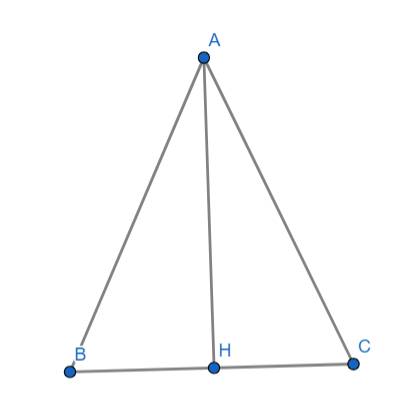
Do tam giác ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến nên:
\(BH=CH=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Xét tam giác vuông ABH ta có:
\(sinB=\dfrac{BH}{AB}\)
\(\Rightarrow sin40^{o0}=\dfrac{2,5}{AB}\Rightarrow AB=\dfrac{2,5}{sin40^o}\approx4\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác đó ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-2,5^2}\approx3\left(cm\right)\)
Đúng 1
Bình luận (0)
