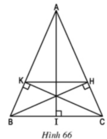
(Tự vẽ hình)
a) Xét \(\Delta BCK\) và \(\Delta CBH\) có:
\(\widehat{BKC}=\widehat{BHC}=90^0\)
\(BC\) chung
\(\widehat{BCH}=\widehat{CBK}\) (tính chất tam giác cân)
\(\Rightarrow\Delta BCK=\Delta CBH\) (ch-gn) \(\Rightarrow BK=CH\)
b) Do \(AB=AC;BK=AH\Rightarrow AB-BK=AC-CH\Rightarrow AK=AH\)
\(\Rightarrow\dfrac{AK}{AB}=\dfrac{AH}{AC}\Rightarrow HK//BC\) (ĐL Ta - let)
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66).
a) Chứng minh BK = CH.
b) Chứng minh KH // BC.
c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.
Cho tam giác ABC (AB=AC). Vẽ đường cao BH, CK
a, chứng minh BK=CH
b,chứng minh KH // BC
c, cho biết BC=a, AB=AC=b. tính HK ?
Cho tam giác ABC cân tại A. Vẽ các đường cao BH và CK.
a) Chứng minh BK = CH
b) Chứng minh KH // BC
c) Cho BC = 10, AB = 8. Tính HK
Cho tam giác ABC cân tại A.Vẽ các đường cao BH và CK (H thuộc AC, K thuộc AB)
a/ Chứng minh tam giác BKC đồng dạng với tam giác CHB theo tỉ số đồng dạng bằng 1
b/ Chứng minh KH // BC
c/ Cho biết BC = a, A B = AC = b. Tính độ dài đoạn thẳng KH theo a và b.
cho tam giác cân ABC (AB=AC) . Vẽ các đường cao BH,CK,AI
a) chứng minh BK=CH
b chứng minh HC.AC=IC.BC
c C/M KH//BC
d cho bt BC =a, AB=AC=b . tính HK theo a và b
Cho tam giác cân ABC (AB=AC), vẽ các đường cao BH, CK (h.60). Chứng minh:
a)BK=CH.
b)KH//BC.
c)Cho biết BC=a,AB=AC=b. Tính độ dài đoạn thẳng HK.
Cho tam giác ABC cân tại A(AB = AC) .Vẽ các đường cao BH , CK, AI của tam giác ABC
a, Chứng minh KH // BC
b, Chứng minh HC.AC = IC.AC
c, Cho biết BC = a, AB = AC= b. Tính độ dài đoạn thẳng HK theo a và b
Cho tam giác cân ABC ( AB = AC ). Vẽ các đường cao BH , CK , AI
a) Chứng minh BK = CH
b) Chứng minh HC.AC = IC.BC
c) Chứng minh KH // BC
d) Cho biết BC = a , AB = b . Tính độ dài đoạn thẳng HK theo a và b
Mn lm giúp mk nha :))
Thanks mn nhiều :))
Cho tam giác ABC cân tại A , có AB= 10cm, BC= 12cm. Vẽ các đường cao AH và BK cắt nhau tại I a) chứng minh ∆AHC đồng dạng với ∆BKC b) tính độ dài CK và diện tích ∆BKC b) chứng minh AI.HK = AK.BI
