Question

Cho tam giác ABC (AB=AC). Vẽ đường cao BH, CK

a, chứng minh BK=CH

b,chứng minh KH // BC

c, cho biết BC=a, AB=AC=b. tính HK ?

Answer 1

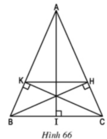
a) Xét ΔKBC vuông tại K và ΔHCB vuông tại H có 

BC chung

\(\widehat{KBC}=\widehat{HCB}\)(hai góc ở đáy của ΔBAC cân tại A)

Do đó: ΔKBC=ΔHCB(cạnh huyền-góc nhọn)

Suy ra: BK=CH(hai cạnh tương ứng)

Answer 2

b) Ta có: AK+KB=AB(K nằm giữa A và B)

AH+HC=AC(H nằm giữa A và C)

mà KB=HC(cmt)

và AB=AC(ΔABC cân tại A)

nên AK=AH

Xét ΔABC có

K\(\in\)AB(gt)

H\(\in\)AC(gt)

\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\left(\dfrac{AK}{AH}=\dfrac{AB}{AC}=1\right)\)

Do đó: KH//BC(Định lí Ta lét đảo)