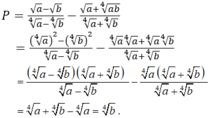Các câu hỏi tương tự
Cho a, b, c là các số thực dương thỏa mãn điều kiện \(\left(a+b-c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}-\dfrac{1}{c}\right)=4\)
Chứng minh \(\left(a^4+b^4+c^4\right)\left(\dfrac{1}{a^4}+\dfrac{1}{b^4}+\dfrac{1}{c^4}\right)\ge2304\)
Cho a, b, c là các số thực dương có tích bằng 1.
Chứng minh rằng \(\sqrt{\dfrac{a^4+b^4}{1+ab}}+\sqrt{\dfrac{b^4+c^4}{1+bc}}+\sqrt{\dfrac{c^4+a^4}{1+ca}}\ge3\)
Cho
∫
1
e
ln
x
(
ln
x
+
x
+
1
)
2
d
x
a...
Đọc tiếp
Cho ∫ 1 e ln x ( ln x + x + 1 ) 2 d x = a e - 2 b e + 4 với a,b là các số nguyên dương. Giá trị của biểu thức b-a bằng
A. 1.
B. 3.
C. -1
D. -3
Biết
∫
0
1
x
d
x
5
x
2
+
4
a
b
với a, b là các số nguyên dương và phân thức a/b là tối giản. Tính giá trị của biểu
T
a
2
+
b...
Đọc tiếp
Biết ∫ 0 1 x d x 5 x 2 + 4 = a b với a, b là các số nguyên dương và phân thức a/b là tối giản. Tính giá trị của biểu T = a 2 + b 2
A. T =13
B. T = 26
C. T = 29
D. T = 34
Cho hai số thực a,b thay đổi thỏa mãn 4a+b-1-(1/2)3a+b-2+5a+3b-4=0. Tìm GTNN của biểu thức P=a2+2ab+b2
Cho số thực dương a. Rút gọn biểu thức
4
a
-
9
a
-
1
2
a
1
2...
Đọc tiếp
Cho số thực dương a. Rút gọn biểu thức 4 a - 9 a - 1 2 a 1 2 - 3 a - 1 2 + a - 4 + 3 a - 1 a 1 2 - a - 1 2
A. 9 a 1 2
B. 9a
C. 3a
D. 3 a 1 2
Biết rằng
∫
4
a
+
b
1
-
x
2
+
6
x
-
5
d
x
π
6
, ở đó a,b là các số nguyên dương và
4
a
+...
Đọc tiếp
Biết rằng ∫ 4 a + b 1 - x 2 + 6 x - 5 d x = π 6 , ở đó a,b là các số nguyên dương và 4 < a + b < 5 . Tổng a+b bằng
A. 5
B. 7
C. 4
D. 6
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a 5b 15-c. Tìm giá trị nhỏ nhất của biểu thức P a2 + b2 + c2 - 4(a+b+c)
Đọc tiếp
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a = 5b = 15-c. Tìm giá trị nhỏ nhất của biểu thức P = a2 + b2 + c2 - 4(a+b+c)
![]()
![]()
![]()
![]()
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)