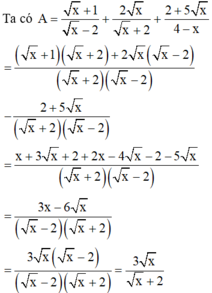Các câu hỏi tương tự
Bài 1: Cho biểu thức P = √x √x x-4 √x−2+√x+2) 2√x (với x > 0 và x ≠ 4) a) Rút gọn biểu thức P b) Tìm x để P = 3 Cho biểu thức P = √x √x x-25 + √x-5 √x+5) 2√x (với x > 0 và x ≠ 25) a) Rút gọn biểu thức P b) Tìm x để P = 2
Cho biểu thức A=2√x - 3/√x - 2 và B=2/√x+3 + √x/√x-3 + 4√x/9-x với x≥0; x≠4; x≠9. a) tính giá trị biểu thức A khi x thỏa mãn |x-2|=2. b) rút gọn biểu thức B. c) đặt C=A.B. Tìm x để C≥1.
√x−4x−2√x+3√x−2�−4�−2�+3�−2 với x 0,x ≠ 4a,Tính giá trị biểu thức A khi x 2b,Chứng minh rằng P B : A 1 - √x
Đọc tiếp
với x > 0,x ≠ 4
a,Tính giá trị biểu thức A khi x = 2
b,Chứng minh rằng P = B : A = 1 -
cho biểu thức A=(3\sqrt(x)+1)/(\sqrt(x)+2) và B=((2)/(\sqrt(x)+2)-(\sqrt(x)-5)/(x-4))-:(\sqrt(x)+1)/(\sqrt(x)-2) (x>=0; x khác 4)
a) tính giá trị biểu thức a khi x =64
b) rút gọn B
c) cho P=A-B tìm x để P có giá trị là số tự nhiên
Cho biết biểu thức A = \(\dfrac{4}{2\sqrt{x}-x}\) B = \(\dfrac{\sqrt{x}-4}{x-2\sqrt{x}}+\dfrac{3}{\sqrt{x}-2}\) với x > 0,x ≠ 4
a,Tính giá trị biểu thức A khi x = 2
b,Chứng minh rằng P = B : A = 1 - \(\sqrt{x}\)
Bài 3. Rút gọn biểu thức: a)x+3+√x² - 6x +9 (x ≤3) b)√x² + 4x +4-√√x² (-2≤x≤0) C)√x²-2x+1 phần x-1 -(x>1) d) x-2/+ √x²-4x+4 x-2 (x1. F,2(a−1) –5a Với a0
Cho \(A=\dfrac{7\sqrt{x}-2}{\sqrt{x}-2}\) và \(B=\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{2}{1-\sqrt{x}}-\dfrac{4\sqrt{x}}{x-1}\) với x ≥ 0, x ≠ 1, x ≠ 4.
a) Tính A khi x = 25.
b) Xét biểu thức P = B - A. Chứng minh: \(P=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\).
c) Tìm x để P = A.B nhận giá trị nguyên lớn nhất.
Cho biểu thức A = 2√x /√x - 2 và B = x/x-4 + 1/√x + 2 với x>0 , x khác 4
a, Tính giá trị của biểu thức A khi x = 9
b, Rút gọn biểu thức B
c, Tìm x nguyên để biểu thức A/B có giá trị là số nguyên
Cho các biểu thức A = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-1}{x-5\sqrt{x}-6};B=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\) với x ≥ 0;x ≠ 4;x ≠ 9
a, Tính giá trị của biểu thức B khi x = 25
b, Rút gọn biểu thức A
c, Tìm các giá trị nguyên của x để A > B
cho biểu thức a=((√x+1)/(√x-1) -(√x+3)/(√x+2))(x-1)/(√x+5) với 0≤x≠1 rút gọn biểu thức a tìm x để a=4/5