Chọn đáp án A
Thể tích của khối hộp chữ nhật có chiều cao bằng h, đáy là hình vuông cạnh a được tính theo công thức:
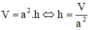 .
.
Diện tích toàn phần của hình hộp là:
![]()
![]()
Chọn đáp án A
Thể tích của khối hộp chữ nhật có chiều cao bằng h, đáy là hình vuông cạnh a được tính theo công thức:
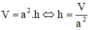 .
.
Diện tích toàn phần của hình hộp là:
![]()
![]()
Một hình hộp chữ nhật có kích thước a (cm) × b (cm) × c (cm), trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi S (cm3) và S (cm2) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = S , tìm số các bộ ba số a , b , c ?
A. 4
B. 10
C. 12
D. 21
Một hình hộp chữ nhật có kích thước a c m × b c m × c c m , trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi V c m 3 và S c m 2 lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = S tìm số các bộ ba số (a,b,c)
A. 4
B. 10
C. 12
D. 21
Một khối hộp chữ nhật ABCD. A 1 B 1 C 1 D 1 có đáy ABCD là một hình vuông. Biết diện tích toàn phần của hình hộp đó là 32, thể tích lớn nhất mà khối hộp ABCD. A 1 B 1 C 1 D 1 là bao nhiêu?
A. 56 3 9
B. 70 3 9
C. 64 3 9
D. 80 3 9
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của khối hộp chữ nhật và khối trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?
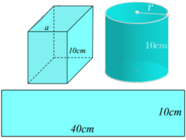
A. 8,3cm.
B. 8,4cm.
C. 8,5cm.
D. 8,6cm.
Xét khối hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là một hình vuông và diện tích toàn phần của hình hộp đó là 32. Thể tích lớn nhất của khối hộp ABCD.A’B’C’ là bao nhiêu?
A. V= 56 3 9
B. V= 70 3 9
C. V= 64 3 9
D. V= 80 3 9
Một hình hộp chữ nhật có ba kích thước là a, b, c. Thể tích V của khối hộp chữ nhật đó bằng
A.(a+b)c
B. 1 3 a b c
C. abc
D.(a+c)b
Một hình hộp chữ nhật có ba kích thước a , b , c . là V Thể tích của khối hộp chữ nhật đó bằng
A. a + c b .
B. a b c .
C. a + b c .
D. 1 3 a b c .
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A ' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. V = 4 a 3 2 3
B. V = 4 a 3 2
C. V = 8 a 3
D. V = 8 a 3 3
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2