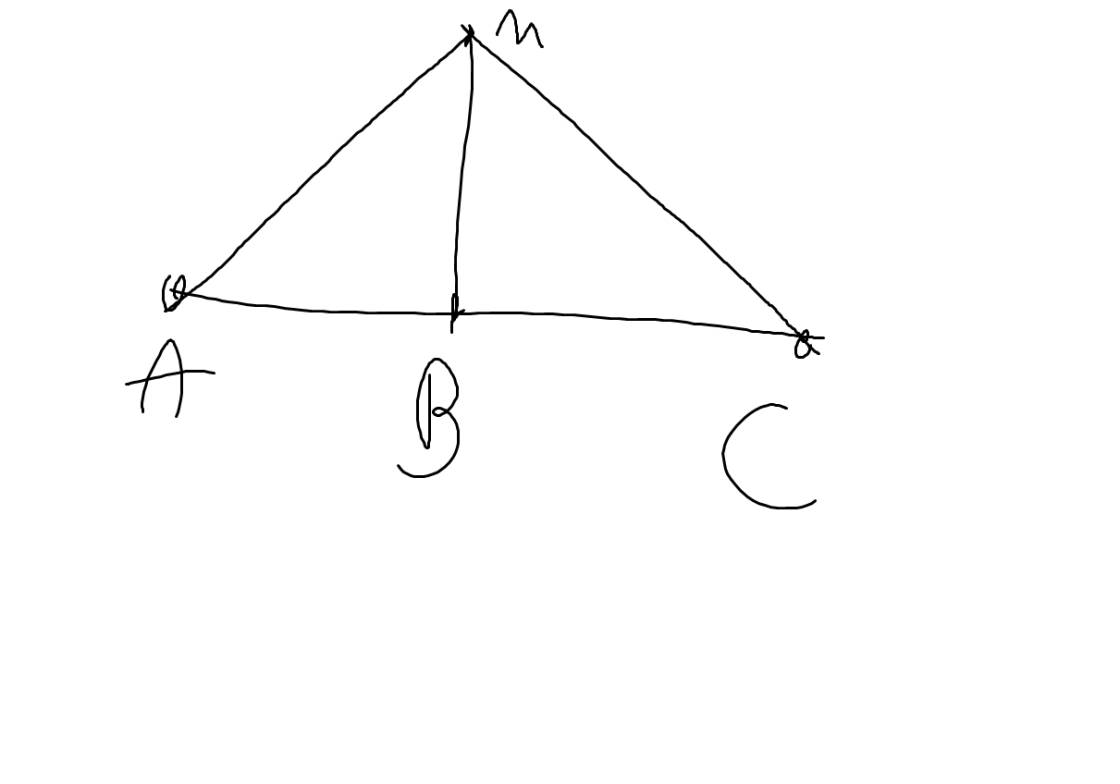
| GT | B nằm giữa A và C BA=4cm; BC=5cm MB\(\perp\)AC tại B |
| KL | a: So sánh MB,MA,MC b: So sánh \(\widehat{MAC};\widehat{MCA}\) c: So sánh \(\widehat{BMA};\widehat{BMC}\) |
a: Ta có: ΔMBA vuông tại B
=>\(MB^2+BA^2=MA^2\)
=>\(MA=\sqrt{MB^2+16}\)
Ta có: ΔMBC vuông tại B
=>\(MB^2+BC^2=MC^2\)
=>\(MC=\sqrt{MB^2+25}\)
Vì \(\sqrt{MB^2+16}< \sqrt{MB^2+25}\)
nên MA<MC
Vì ΔMBA vuông tại B
nên MB<MA
=>MB<MA<MC
b: Xét ΔMAC có MA<MC
mà \(\widehat{MCA};\widehat{MAC}\) lần lượt là góc đối diện của cạnh MA,MC
nên \(\widehat{MCA}< \widehat{MAC}\)
c: Ta có: \(\widehat{BMA}+\widehat{MAB}=90^0\)(ΔMAB vuông tại B)
\(\widehat{BMC}+\widehat{MCB}=90^0\)(ΔMBC vuông tại B)
mà \(\widehat{MAB}>\widehat{MCB}\)
nên \(\widehat{BMA}< \widehat{BMC}\)














