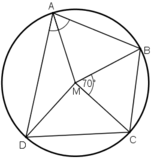
Ta có:
![]() (1)
(1)
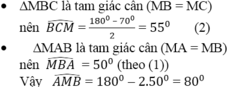 (3)
(3)
![]() (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
(số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
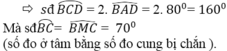
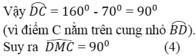
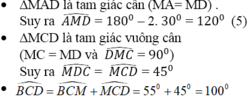
(theo (2) và (6) và Cm là tia nằm giữa hai tia CB,CD).

Ta có:
![]() (1)
(1)
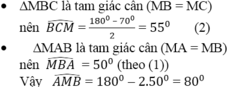 (3)
(3)
![]() (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
(số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
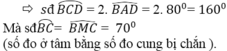
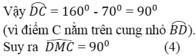
(theo (2) và (6) và Cm là tia nằm giữa hai tia CB,CD).
Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn kẻ các tiếp tuyến MA,MB với đường tròn( A,B các tiếp điểm) kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D ) a)C/M tứ giác MAOB nội tiếp b) C/M MA^2 =MC.MD c) Gọi H là giao điểm của AB và MO. CM tứ giác CHOD nội tiếp
Từ điểm M nằm bên ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA,MB đến đường tròn (O) ( AB là các tiếp điểm và C nằm giữa M, D)
a) C/m MA bình= MC.MD
b) Gọi I là trung điểm của CD. C/m 5 điểm M, A, O, I, B cùng nằm trên một đường tròn.
c) Gọi H là giao điểm của AB và MO. C/m tứ giác CHOD nội tiếp đường tròn
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). C/m A,B,K thẳng hàng.
Cho đường tròn tâm O bán kính R và điểm M nằm ngoài đường tròn. Từ M vẽ hai tiếp tuyến MA, MB với đường tròn (A,B là hai tiếp tuyến) a) Chứng minh tứ giác MAOB là nội tiếp trong một đường tròn b) Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Chứng minh hệ thức MA^2 = MC.MD c) Gọi H là trung điểm của dây CD. Chứng minh HM là tia phân giác của góc AHB giúp em với ạ em đang cần gấp
BÀI 1 cho tam giác ABC vuông tại A .Nữa đường tròn đường kính AB cắt BC tại D.Trên cung AD lấy một điểm E .Nối BE và kéo dài AC tại F.Chứng minh tứ giác CDEF nội tiếp
BÀI 2: Cho đường tròn tâm O đường kính AB cố định ,CD là đường kính thay đổi của đường tròn (O) ( khác AB ) .Tiếp tuyến tại B của (O ) cắt AC và AD lần lượt tại N và M .Chứng minh tứ giác CDMN nội tiếp
BÀI 3 :Cho hai đoạn thẳng MN và PQ cắt nhau tại O .Biết OM.ON= PO.OQ.Chứng minh tứ giác MNPQ nội tiếp
BÀI 4: Cho tam giác ABC có đường cao AH . Gọi M, N lần lượt là hình chiếu vuông góc của H lên các cạnh AB, AC
a) c/m AMHN nội tiếp
b) BMNC nội tiếp
BÀI 5: Cho tam giác ABC các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N .chứng minh BMCN nội tiếp
BÀI 6: Cho đường tròn (O) đường kính AB .Gọi M là một điểm trên tiếp tuyến xBy , đường thẳng AM cắt đường tròn (O) tại C , lấy D thuộc BM, nối AD cắt (O) tại I. c/m CIDM nội tiếp
BÀI 7: Cho đường tròn tâm (O) có cung EH và S là điểm chính giữa cung đó .Trên dây EH lấy hai điểm A và B .Các đường thẳng SA và SB cắt đường tròn lần lượt tại D và C .c/m ABCD là tứ giác nội tiếp
BÀI 8: Cho đường tròn (O) đường kính AB , từ A và B vẽ Ax vuông góc AB và By vuông góc BA (Ax và By cùng phía so với bờ AB ) .Vẽ tiếp tuyến x'My' (tiếp điểm M) cắt Ax tại C và By tại D ; OC cắt AM tại I và OD cắt BM tại K .Chứng minh CIKD nội tiếp
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.
a> C/m tứ giác BIKD nội tiếp
b> C/m IK//BC
c> Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IE=ID.CE( với E là giao điểm của BK và ID)
d> Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
a)Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MC của đường tròn, A và C là các tiếp điểm. Kẻ đường kính BC. Biết 70 độ thì góc AMC bằng:
b)Cho đường tròn (O; 2cm). Từ điểm A sao cho OA = 4cm , vẽ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Chu vi tam giác ABC bằng:
c)Cho nửa đường tròn tâm O, đường kính AB cm =10 . Điểm M thuộc nửa đường tròn. Qua M kẻ tiếp tuyến xy với nửa đường tròn. Gọi D và C lần lượt là hình chiếu của A, B trên xy. Diện tích lớn nhất của tứ giác ABCD là:
Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh: a) Tứ giác ABHM nội tiếp b) OA.OB = OH.OM = R2 c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất
Bài 1:Từ điểm M nằm ngoài đường tròn (O). Vẽ các tiếp tuyến AM,BM với đường tròn (A,B là các tiếp điểm) và cát tuyến MCD không đi qua tâm O (C nằm giữa M và D) với đường tròn(O).
a)C/m: Tứ giác MAOB nội tiếp
b)C/m: MA2=MC.MD
c)Đường thẳng MO cắt AB tại H và cắt (O) tại I và K( I nằm giữa M và K).C/m: CK là tia phân giác của góc DCH
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Cho đường tròn tâm O, bán kính R và M là một điểm nằm bên ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Gọi E là giao điểm của AB và OM.
a) Chứng minh tứ giác MAOB nội tiếp được trong một đường tròn.
b) Tính độ dài đoạn thẳng AB và ME biết OM = 5cm và R = 3cm.
c) Kẻ tia Mx nằm trong góc AMO cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D). Chứng minh rằng góc MEC = góc OED