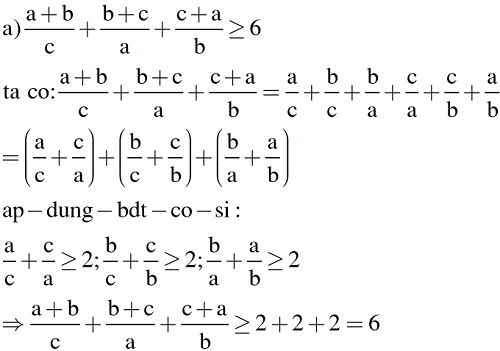\(\dfrac{a+b}{c}+\dfrac{a+c}{b}+\dfrac{b+c}{a}\)
\(=\dfrac{a}{c}+\dfrac{b}{c}+\dfrac{a}{b}+\dfrac{c}{b}+\dfrac{b}{a}+\dfrac{c}{a}\)
\(=\left(\dfrac{a}{c}+\dfrac{c}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{a}{b}+\dfrac{b}{a}\right)\)
Áp dụng BĐT cô si, ta có:
\(\left(\dfrac{a}{c}+\dfrac{c}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{a}{b}+\dfrac{b}{a}\right)\)
\(\ge2\sqrt{\dfrac{a}{c}.\dfrac{c}{a}}+2\sqrt{\dfrac{b}{c}.\dfrac{c}{b}}+2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2+2+2=6\left(đpcm\right)\)