Các câu hỏi tương tự
Cho tam giác ABC vuông ở đỉnh A. Trên cạnh AC lấy điểm M (khác với A và C). Vẽ đường tròn (O) đường kính MC. Gọi N là giao điểm thứ 2 của cạnh BC với đường tròn (O). Nối BM và kéo dài, cắt đường tròn (O) tại điểm thứ hai là P. 1) Chứng minh rằng tứ giác AMNB là tứ giác nội tiếp. 2) Chứng minh rằng hai tam giác ABP và MNP đòng dạng. 3) Đường thẳng AP cắt đường tòn (O) tại điểm thứ 2 là D (khác P). Đường thẳng ND cắt các đường thẳng AC và PC lần lượt tại E và G. Chứng minh rằng CM.CE CP.CG
Đọc tiếp
Cho tam giác ABC vuông ở đỉnh A. Trên cạnh AC lấy điểm M (khác với A và C). Vẽ đường tròn (O) đường kính MC. Gọi N là giao điểm thứ 2 của cạnh BC với đường tròn (O). Nối BM và kéo dài, cắt đường tròn (O) tại điểm thứ hai là P. 1) Chứng minh rằng tứ giác AMNB là tứ giác nội tiếp. 2) Chứng minh rằng hai tam giác ABP và MNP đòng dạng. 3) Đường thẳng AP cắt đường tòn (O) tại điểm thứ 2 là D (khác P). Đường thẳng ND cắt các đường thẳng AC và PC lần lượt tại E và G. Chứng minh rằng CM.CE = CP.CG
Tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M, vẽ đường tròn đường kính MC cắt BC tại (D khác C) và cắt đường thẳng BM tại E ( E khác M). Đường thẳng AE cắt đường tròn tại S (S khác E). Chứng minh:
a) AM.MC=BM.ME
b) CA là tia phân giác góc SCB
c) Tam giác MDS cân
Cho tam giác ABC vuông tại A (AB lớn hơn AC) trên cạnh AC lấy M (khác A và C). Đường tròn đường kính MC cắt BC tại E và cắt đường thẳng BM tại D (E khác C, D khác M)a) Chứng minh tứ giác ABCD nội tiếp b) Chứng minh góc ABD bằng góc MEDc) Đường thẳng AD cắt đường tròn đường kính MC tại N (N khác D). Chứng minh CA là phân giác của góc NCEd) Đường thẳng MD cắt CN tại K, MN cắt CD tại H. Chứng minh KH song song NEGiải giúp em câu c, d nha
Đọc tiếp
Cho tam giác ABC vuông tại A (AB lớn hơn AC) trên cạnh AC lấy M (khác A và C). Đường tròn đường kính MC cắt BC tại E và cắt đường thẳng BM tại D (E khác C, D khác M)
a) Chứng minh tứ giác ABCD nội tiếp
b) Chứng minh góc ABD bằng góc MED
c) Đường thẳng AD cắt đường tròn đường kính MC tại N (N khác D). Chứng minh CA là phân giác của góc NCE
d) Đường thẳng MD cắt CN tại K, MN cắt CD tại H. Chứng minh KH song song NE
Giải giúp em câu c, d nha
cho tam giác ABC vuông tại A (AB>AC). Trên cạnh AC lấy điểm M khác A và C. Vẽ đường tròn đường kính MC cắt BC tại E và cắt đường thẳng MB tại D (E khác C và D khác M)
a. C/m ABCD nội tiếp
b. C/m góc ABD = góc MED
c. Đường thẳng AD cắt đường tròn đường kính MC tại N. Đường thẳng MD cắt Cn tại K. MN cắt CD tại H. C/m KH//NE
cho tam giác ABC vuông tại A (AB>AC). Trên cạnh AC lấy điểm M khác A và C. Vẽ đường tròn đường kính MC cắt BC tại E và cắt đường thẳng MB tại D (E khác C và D khác M)
a. C/m ABCD nội tiếp
b. C/m góc ABD = góc MED
c. Đường thẳng AD cắt đường tròn đường kính MC tại N. Đường thẳng MD cắt Cn tại K. MN cắt CD tại H. C/m KH//NE
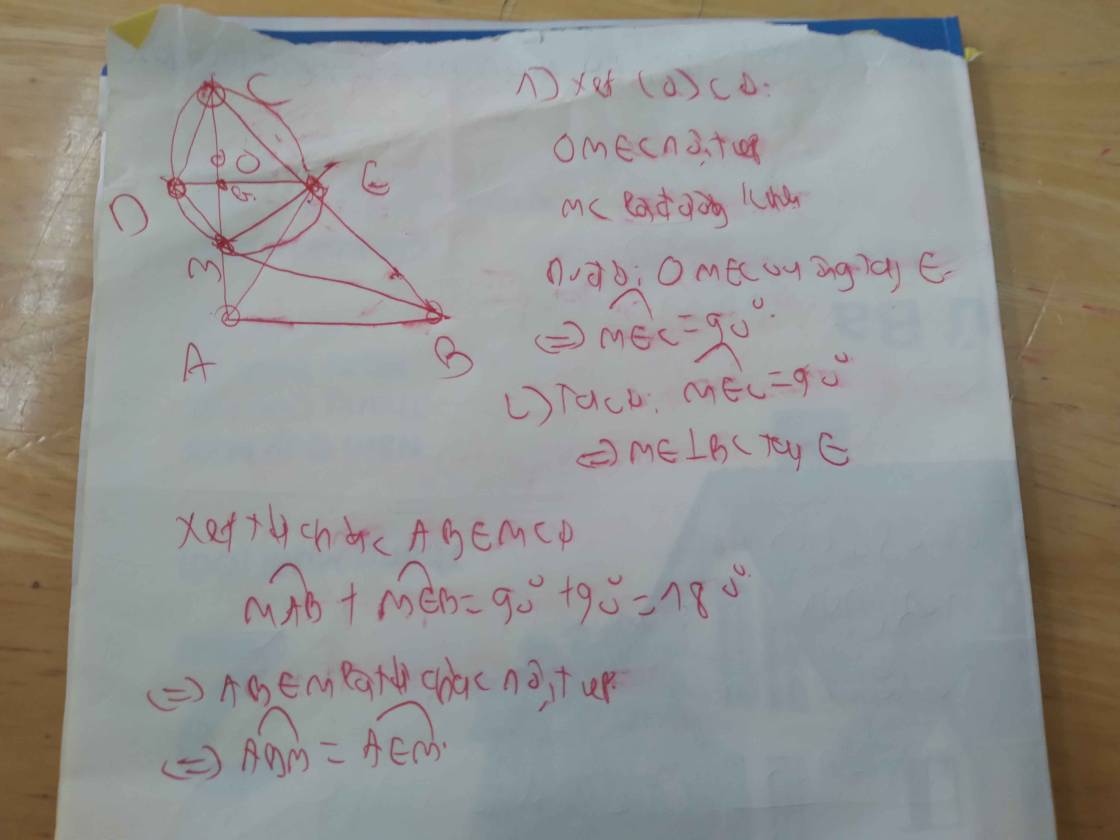
Bài 3. Cho tam giác ABC vuông ở A, với AC AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Đọc tiếp
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Cho tam giác ABC vuông tại A. Trên cạnh AB lấy M sao cho góc MCB nhỏ hơn góc MCA. Đường tròn đường kính MC cắt cạnh BC tại D. Đường thẳng MD cắt đường thẳng AC tại E.a)Chứng minh EADB là tứ giác nội tiếp (đã làm).b) Trên đường tròn đường kính MC lấy điểm H sao cho M là trung điểm của cung DH, chứng minh HD // EB.(đã làm).c) Gọi N là giao điểm của các đường thẳng MC và EB, chứng minh N,H,A thẳng hàng.LÀM GIÚP MÌNH CÂU C VỚI
Đọc tiếp
Cho tam giác ABC vuông tại A. Trên cạnh AB lấy M sao cho góc MCB nhỏ hơn góc MCA. Đường tròn đường kính MC cắt cạnh BC tại D. Đường thẳng MD cắt đường thẳng AC tại E.
a)Chứng minh EADB là tứ giác nội tiếp (đã làm).
b) Trên đường tròn đường kính MC lấy điểm H sao cho M là trung điểm của cung DH, chứng minh HD // EB.(đã làm).
c) Gọi N là giao điểm của các đường thẳng MC và EB, chứng minh N,H,A thẳng hàng.
LÀM GIÚP MÌNH CÂU C VỚI
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.a. Chứng minh OA vuông góc với BC tại H.b. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn(O) tại E (E khác D). Chứng minh: AE.AD AC^2c. Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh rằng FD là tiếp tuyến của đường tròn (O).
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a. Chứng minh OA vuông góc với BC tại H.
b. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn(O) tại E (E khác D). Chứng minh: AE.AD = AC^2
c. Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh rằng FD là tiếp tuyến của đường tròn (O).
Cho tam giác abc có ba góc nhọn nội tiếp đường tròn tâm O Trên cạnh BC lấy điểm d d khác B phẩy C sao cho đường thẳng vuông góc với BC tại D cắt cung nhỏ AC tại đường tròn tâm O tại M Gọi E là hình chiếu của M trên AC
a Chứng minh tứ giác CDME nội tiếp đường tròn
b/chứng minh MA x MB = MB x ME
C/Gọi i k lần lượt là trung điểm của AB và de chứng minh EK vuông góc với MK