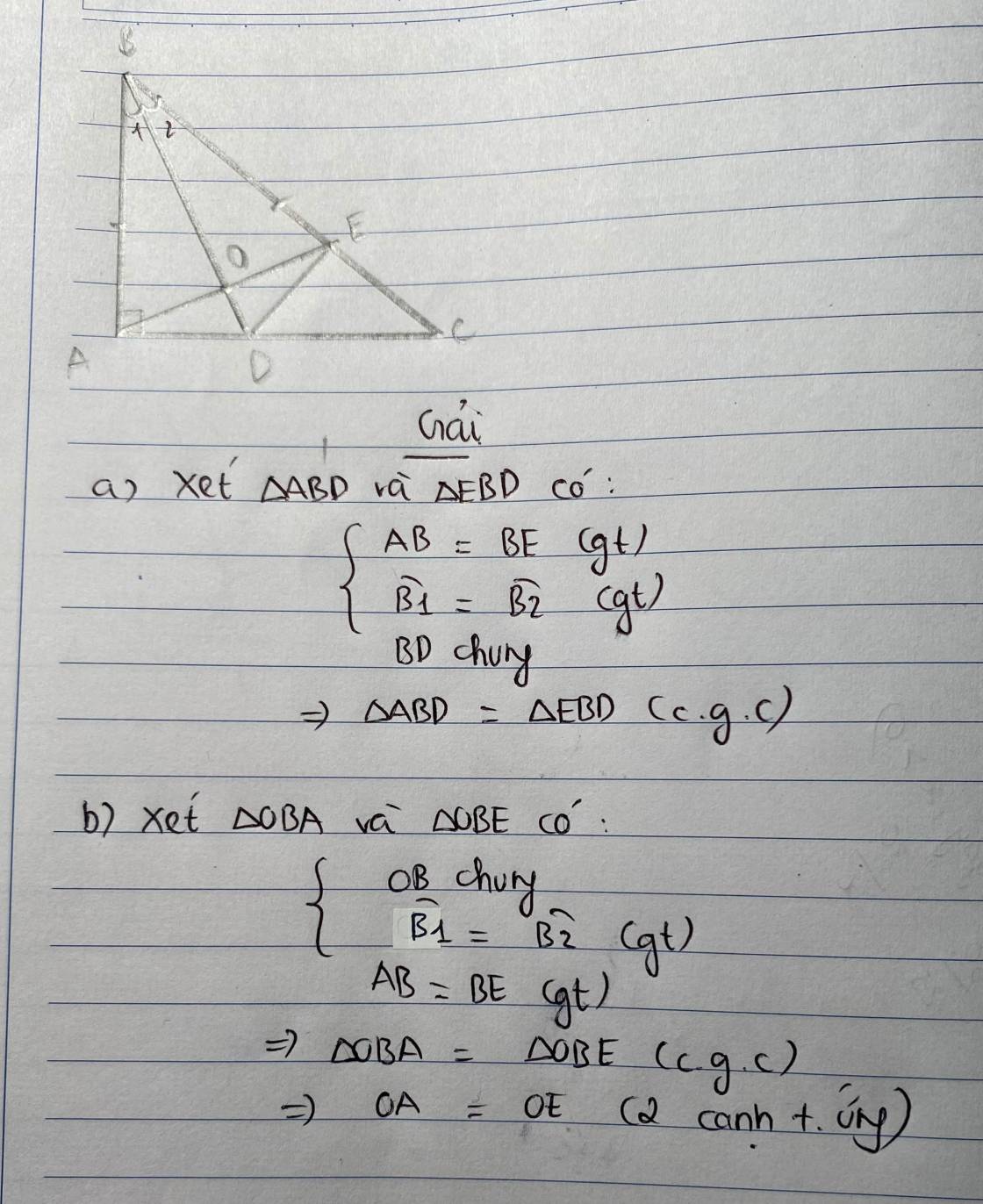Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, vẽ BD là tia phân giác của ABC (D thuộc AC. Trên cạnh BC lấy điểm E sao cho BE=BA. Gọi I là giao điểm của BD và AE. a) Chứng minh: tam giác ABD= tam giác EBD. b) Chứng minh: DE=AD và DE vuông góc BC.
cho tam giác abc vuông tại a có bd là phân giác của góc abc ( dthuộc ac ) trên cạnh bc lấy điểm e sao cho be=ba cm tam giác abd = tam giác ebd b> họi o là giao điểm của ae và bd cm oa=oe
Cho tam giác ABC vuông tại A có BD là tia phân giác của ABC(D thuộc AC).Trên cạnh BC lấy điểm E cho BE = BA
a. Chứng minh tam giác ABD bằng tam giác EBD
b. Gọi O là giao điểm của AE và BD .chứng minh OA = OE
Giúp mik nha mik đag cần gấp
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BABE. Tia phân giác của góc B cắt AC tại D
a) Chứng minh tam giác ABD tam giác EBD
b) Chứng minh BD là đường trung trực của AE
c) Kẻ AH vuông góc BC ( H thuộc BC ). Chứng minh AH //DE
d) Chứng minh góc ABCgóc EDC ( gợi ý: sử dụng tính chất 2 góc nhọn phụ nhau trong 2 tam giác vuông )
e) Gọi K là giao điểm của ED và BA. M là trung điểm của KC. Chứng minh B, D, M thẳng hàng
🤒🤒ÉT O ÉTTTTTT
Đọc tiếp
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BA=BE. Tia phân giác của góc B cắt AC tại D
a) Chứng minh tam giác ABD= tam giác EBD
b) Chứng minh BD là đường trung trực của AE
c) Kẻ AH vuông góc BC ( H thuộc BC ). Chứng minh AH //DE
d) Chứng minh góc ABC=góc EDC ( gợi ý: sử dụng tính chất 2 góc nhọn phụ nhau trong 2 tam giác vuông )
e) Gọi K là giao điểm của ED và BA. M là trung điểm của KC. Chứng minh B, D, M thẳng hàng
🤒🤒ÉT O ÉTTTTTT
4)ch tam giác ABC vuông tại A và AB<AC . trên cạnh BC lấy điểm E sao cho BE=BA, kẻ BD là tia phân giác của góc ABC( D thuộc AC)
a)chứng minh: tam giác ABC= tam giác EBD
b)chứng minh: DE vuông góc BC
c)Gọi K là giao điểm của BA và ED. Chứng minh: BK = BC
5)so sánh 2 số : \(^{2^{300}}\) và \(3^{200}\)
Cho tam giác ABC vuông tại A và AB < AC. Trên cạnh BC lấy điểm E sao cho BE= BA, kẻ BD là tia phân giác của góc ABC (D thuộc AC).
a) Chứng minh: ∆ABD = ∆EBD
b) Chứng minh: DE vuông góc với BC
c) Gọi K là giao điểm của BA và ED. Chứng minh: BK = BC
Cho tam giác ABC vuông tại A (AB < AC). Kẻ tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho: BE = AB. 1) Chứng minh rằng: ∆ABD = ∆EBD; 2) Gọi giao điểm của BD và AE là I. Hỏi I có là trung điểm của AE không? Vì sao? 3) Kéo dài ED cắt AB tại K. Chứng minh: AK = EC và AE // KC.
Cho tam giác ABC vuông tại A,tia phân giác của góc ABC cắt AC tại D.Trên cạnh BC lấy điểm E sao cho BE=BA
a)Chứng minh tam giác ABD=tam giác EBD
b)Chứng minh BD là đường trung trực của AE
c)Gọi F là giao điểm của AB và DE.Chứng minh BF=BC
Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh
a) OAM OBM;
b) AM BM; OM AB
c) OM là đường trung trực của AB
d) Trên tia Ot lấy điểm N . Chứng minh NA NB
Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng:
a) AB // KE b) ABC KEC ; BC CE
Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C....
Đọc tiếp
\(Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK = CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng: a) AB // KE b) ABC = KEC ; BC = CE Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD. a) Chứng minh: AD = BC. b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD c) Chứng minh: OE là phân giác của góc xOy, OE CD Bài 4. Cho ABC coù BÂ=900, gọi M là trung điểm của BC. Trên tia đối của tia AM lấy điểm E sao cho ME = MA. a) Tính BCE b) Chứng minh BE // AC. Bài 5. Cho ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi Mlà trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng: a) AME = DMB; AE // BC b) Ba điểm E, A, F thẳng hàng c) BF // CE Bài 6: Cho có B = C , kẻ AH BC, H BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) AB = AC b) ABD = ACE c) ACD = ABE d) AH là tia phân giác của góc DAE e) Kẻ BK AD, CI AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm. \)
Bài 2. Cho ABC có A 120°. Tia phân giác của A cắt BC tại D. Tia phân giác củaADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,BC, AD. Chứng minh:a) AC là tia phân giác của DAH .b) IH IKBài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI HK. Chứngminh:a) Chứng minh AB //HKb) Chứng minh KAH IAH c) Chứng minh AKI cânBài 7. Cho ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấ...
Đọc tiếp
Bài 2. Cho ABC có A = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác của
ADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,
BC, AD. Chứng minh:
a) AC là tia phân giác của DAH .
b) IH = IK
Bài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH
AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng
minh:
a) Chứng minh AB //HK
b) Chứng minh KAH IAH
c) Chứng minh AKI cân
Bài 7. Cho ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao
cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD b) BMD = CME
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh
MN / / AC //BD.
Bài 8. Cho xOy . Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D
thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC
Chứng minh.:
a) AD = BC b) ABE = CDE
c) OE là tia phân giác của góc xOy