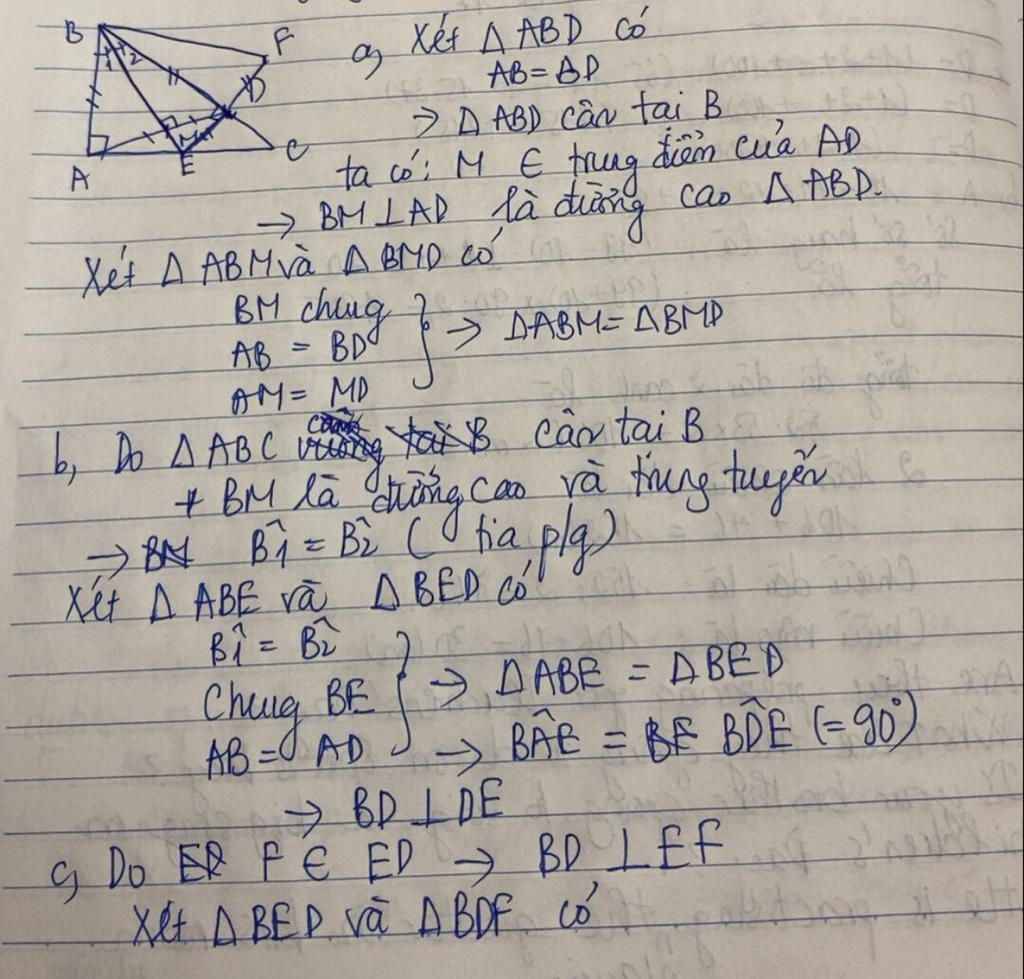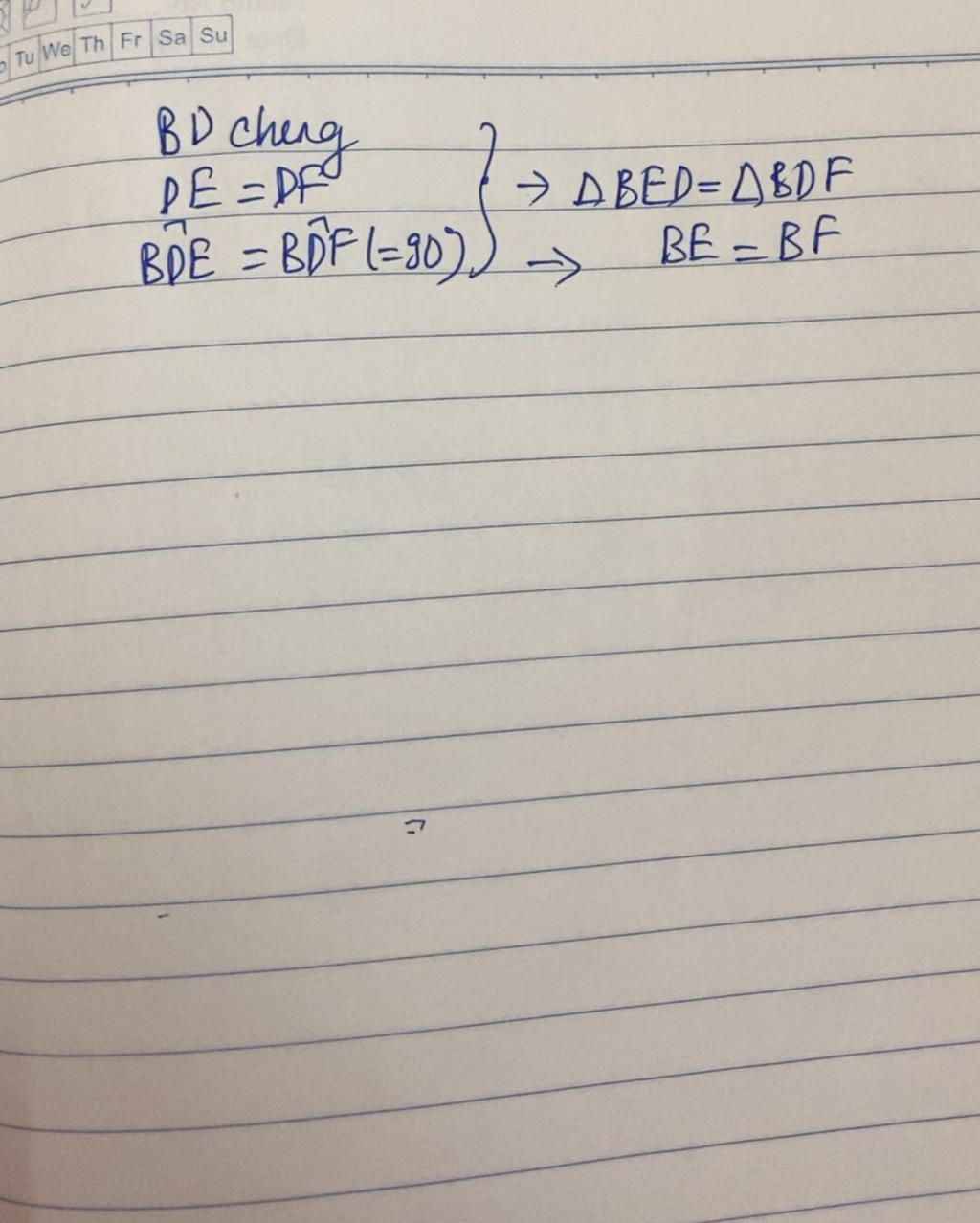Question

Cho ∆ ABC vuông tại A ( AB < AC), có BE là đường phân giác.
Trên cạnh BC lấy điểm D sao cho BD = BA.
a) Chứng minh: ∆  ABD cân và BE vuông AD

b) Chứng minh: ∆BAE = ∆ BDE và EA = ED.
c) Trên tia BA lấy điểm F sao cho AF = DC. Chứng minh: EF = EC.
d) Chứng minh: F, E, D thẳng hàng.

Answer 1

Answer 2

a) Vì AB=BD 

=> tam giác ABD cân tại B

mà BE là đường phân giác 

=> BE đồng thời là đường cao

=> BE⊥AD

b) Xét tam giác ABE và tam giác DBE có:

AB=BD (gt)

góc ABE= góc DBE (BE là phân giác góc ABC)

BE: cạnh chung

=> tam giác BAE= tam giác BDE(c.g.c)

=> EA=ED và góc A=D=90 độ

c) Xét tam giác AFE và DCE có:

AF=DC (gt)

góc A= góc D= 90 độ (cmt)

AE=DE (cmt)

=> tam giác AFE=DCE(c.g.c)

=> EF=EC

d) Nếu chứng minh F, E, D thẳng hàng thì đề câu c là trên tia đối tia AB lấy điểm F sao cho AF=DC

vì tam giác AFE=DCE(c.g.c)

=> góc AEF= góc DEC

mà góc DEC + góc AED= 180 độ

=> góc AEF +góc AED=180 độ

=> F, E, D thẳng hàng