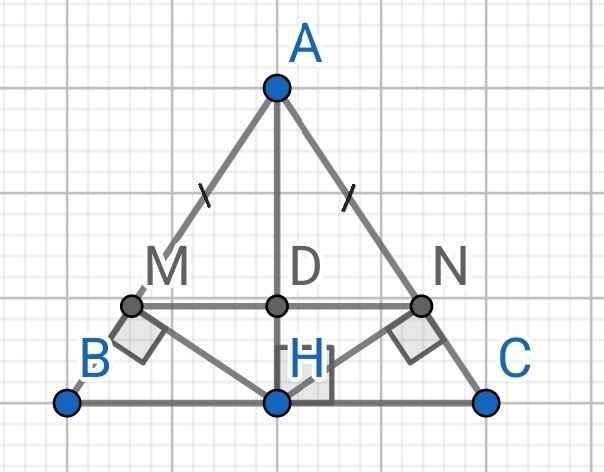
a) Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AB = AC (gt)
AH là cạnh chung
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
b) Do ∆ABH = ∆ACH (cmt)
⇒ ∠BAH = ∠CAH (hai góc tương ứng)
⇒ ∠MAH = ∠NAH
Xét hai tam giác vuông: ∆AMH và ∆ANH có:
AH là cạnh chung
∠MAH = ∠NAH (cmt)
⇒ ∆AMH = ∆ANH (cạnh huyền - góc nhọn)
c) Do ∆AMH = ∆ANH (cmt)
⇒ MH = NH (hai cạnh tương ứng)
Do ∆ABH = ∆ACH (cmt)
⇒ BH = CH (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆MBH và ∆NCH có:
BH = CH (cmt)
MH = NH (cmt)
⇒ ∆MBH = ∆NCH (cạnh huyền - cạnh góc vuông)
d) Do ∆AMH = ∆ANH (cmt)
⇒ ∠MHA = ∠NHA (hai góc tương ứng)
⇒ HA là tia phân giác của ∠MHN
e) Gọi D là giao điểm của MN và AH
Do ∆AMH = ∆ANH (cmt)
⇒ ∠MAH = ∠NAH (hai góc tương ứng)
⇒ ∠MAD = ∠NAD
Do ∆AMH = ∆ANH (cmt)
⇒ AM = AN (hai cạnh tương ứng)
Xét ∆AMD và ∆AND có:
AM = AN (cmt)
∠MAD = ∠NAD (cmt)
AD là cạnh chung
⇒ ∆AMD = ∆AND (c-g-c)
⇒ ∠AMD = ∠AND (hai góc tương ứng)
⇒ ∠AMN = ∠ANM
∆AMN có:
∠AMN + ∠ANM + ∠MAN = 180⁰ (tổng ba góc trong ∆AMN)
⇒ ∠AMN = ∠ANM = (180⁰ - ∠MAN) : 2
= (180⁰ - BAC) : 2 (1)
Do ∆ABH = ∆ACH (cmt)
⇒ ∠ABH = ∠ACH (hai góc tương ứng)
⇒ ∠ABC = ∠ACB
∆ABC có:
∠BAC + ∠ABC + ∠ACB = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (2)
Từ (1) và (2) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC













