Xét \(\Delta ABD\) và \(\Delta ACE\) ta có :
\(\left\{{}\begin{matrix}AB=AC\\\widehat{ABD}=\widehat{ACE}=90^o\end{matrix}\right.\)
Vậy \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
`->DE``//``//``BC`
Ta có : \(\widehat{ABC}=\widehat{ACB}\)
\(\rightarrow\widehat{EBC}=\widehat{DCB}\)
Nên `BEDC` là hình thang cân ( tứ giác có `2` cạnh đối song song là hình thang , hình thang có `2` góc kề một đáy bằng nhau là hình thang cân )
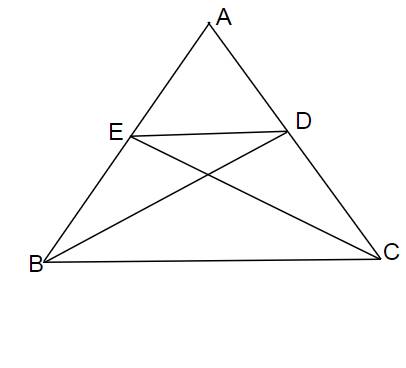
Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
Xét ΔABC có AD/AC=AE/AB
nên DE//BC
=>BEDC là hình thag
mà góc EBC=góc DCB
nên BEDC là hình thang cân















