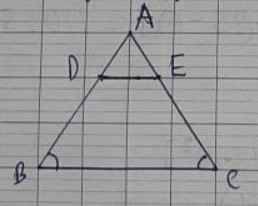
Ta có:
\(\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân=A\right)\Rightarrow\dfrac{AB}{AC}=1\\AD=AE\left(gt\right)\Rightarrow\dfrac{AD}{AE}=1\end{matrix}\right.\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE}\)
Mà \(\widehat{BAC}=\widehat{DAE}\left(góc.chung\right)\)
Nên \(\Delta ABC\sim\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{ADE}\)
\(\Rightarrow DE//BC\) (2 góc đồng vị bằng nhau)
Xét tứ giác `BDEC` có: DE//BC
\(\Rightarrow\) Tứ giác BDEC là hình thang
Mà \(\widehat{DBC}=\widehat{ECB}\) (ΔABC cân tại A)
Nên hình thang BDEC là hình thang cân.
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>BDEC là hình thang
mà góc B=góc C
nên BDEC là hình thang cân














