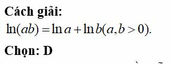Các câu hỏi tương tự
Cho
I
∫
1
e
ln
x
x
ln
x
+
2
2
d
x
có kết quả dạng
I
ln
a...
Đọc tiếp
Cho I = ∫ 1 e ln x x ln x + 2 2 d x có kết quả dạng I = ln a + b với a > 0 , b ∈ ℚ . Khẳng định nào sau đây đúng?
A. 2ab = -1
B. 2ab = 1
C. - b + ln 3 2 a = - 1 3
D. b + ln 3 2 a = 1 3
Đặt
a
ln
2
,
b
ln
5
, hãy biểu diễn
I
ln
1
2
+
ln
2
3
+
.
.
.
+
ln
98
99
+
ln
99
100
theo a và b. A.
I
-...
Đọc tiếp
Đặt a = ln 2 , b = ln 5 , hãy biểu diễn I = ln 1 2 + ln 2 3 + . . . + ln 98 99 + ln 99 100 theo a và b.
A. I = - 2 a - b
B. I = 2 a + b
C. I = - 2 a + b
D. I = 2 a - b
Cho
a
l
o
g
3
,
b
l
n
3.
Mệnh đề nào sau đây đúng A.
a
b
e
10
B.
10
a
e
b
C.
1
a
+
1...
Đọc tiếp
Cho a = l o g 3 , b = l n 3. Mệnh đề nào sau đây đúng
A. a b = e 10
B. 10 a = e b
C. 1 a + 1 b = 1 10 e
D. 10 b = e a
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Biết
I
∫
1
3
x
+
2
x
d
x
a
+
b
ln
c
,với
a
,
b
,
c
∈
ℤ
,
c
9.
Tính tổng
S
a
+
b
+
c
. A. ...
Đọc tiếp
Biết I = ∫ 1 3 x + 2 x d x = a + b ln c ,với a , b , c ∈ ℤ , c < 9. Tính tổng S = a + b + c .
A. S = 7.
B. S = 5.
C. S = 8.
D. S = 6.
Với a, b là hai số thực khác 0 tùy ý, l n ( a 2 b 4 ) bằng
A. 2ln|a|+4ln|b|
B. 4(ln|a|+ln|b|)
C. 2lna+4lnb
D. 4lna+2lnb
Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng A.
ln
a
.
ln
(
a
b
)
B.
ln
a
+
ln
(
1
+
b
)
C.
ln
a
ln
(
1...
Đọc tiếp
Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng
A. ln a . ln ( a b )
B. ln a + ln ( 1 + b )
C. ln a ln ( 1 + b )
D. ln a + ln a b
Với a,b 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của
P
a
4
+
b
4
bằng A.
2
+
1
4
.
B.
2
2...
Đọc tiếp
Với a,b > 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của P = a 4 + b 4 bằng
A. 2 + 1 4 .
B. 2 2 − 1 4 .
C. 2 − 1 4 .
D. 2 2 + 1 4 .
Tính tích phân
I
∫
1
2
1
x
x
+
1
2
d
t
ln
a
+
b
. Khi đó S a +2b bằng: A.
2
3
B.
-
2
3
C. 1 D. - 1
Đọc tiếp
Tính tích phân I = ∫ 1 2 1 x x + 1 2 d t = ln a + b . Khi đó S = a +2b bằng:
A. 2 3
B. - 2 3
C. 1
D. - 1
Biết
∫
1
3
2
+
ln
(
x
+
3
)
(
x
+
1
)
2...
Đọc tiếp
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 dx =a ln2+b ln3+c (a,b,c∈Q). Giá trị 3a-b+2c bằng
A. 7.
B. 0.
C. -2.
D. -11/2