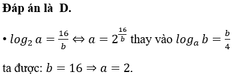Các câu hỏi tương tự
Cho a 0,b 0 và a khác 1 thỏa mãn
log
a
b
b
4
;
log
2
a
16
b
. Tính tổng a+b A. 12 B. 10 C. 18 D. 16
Đọc tiếp
Cho a >0,b >0 và a khác 1 thỏa mãn log a b = b 4 ; log 2 a = 16 b . Tính tổng a+b
A. 12
B. 10
C. 18
D. 16
Trong không gian Oxyz, cho các điểm A(2 ;1 ;0),B(0 ;4 ;0),C(0,2,-1) Biết đường thẳng ∆ vuông góc với mặt phẳng (ABC) và cắt đường thẳng
d
:
x
-
1
2
y
+
1
1
z
-
2
3
tại điểm D(a ;b ;c) thỏa mãn a 0 và tứ di...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(2 ;1 ;0),B(0 ;4 ;0),C(0,2,-1) Biết đường thẳng ∆ vuông góc với mặt phẳng (ABC) và cắt đường thẳng d : x - 1 2 = y + 1 1 = z - 2 3 tại điểm D(a ;b ;c) thỏa mãn a > 0 và tứ diện ABCD có thể tích bằng 17/6. Tổng a+b+c bằng
A. 5
B. 4
C. 7
D. 6
Cho a, b 0, a ≠ 1 thỏa mãn
log
a
b
b
4
và
log
2
a
16
b
. Tổng a + b bằng: A. 16 B. 17 C. 18 D. 19
Đọc tiếp
Cho a, b > 0, a ≠ 1 thỏa mãn log a b = b 4 và log 2 a = 16 b . Tổng a + b bằng:
A. 16
B. 17
C. 18
D. 19
Cho a;b;c là ba số thực dương,
a
1
và thỏa mãn
log
2
a
b
c
+
log
a
b
3
c
3
+
b
c...
Đọc tiếp
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Cho các số thực a;b;c;d thay đổi, luôn thỏa mãn
a
-
1
2
+
b
-
2
2
1
và
4
c
-
3
d
-
23
0
. Giá trị nhỏ nhất của biểu thức
P
:...
Đọc tiếp
Cho các số thực a;b;c;d thay đổi, luôn thỏa mãn a - 1 2 + b - 2 2 = 1 và 4 c - 3 d - 23 = 0 . Giá trị nhỏ nhất của biểu thức P : a - c 2 + b - d 2 là:
A. P m i n = 28
B. P m i n = 3
C. P m i n = 4
D. P m i n = 16
Cho các số thực a, b, c thỏa mãn
2
a
6
b
12
-
c
và
a
-
1
2
+
b
-
1
2
+
c...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn 2 a = 6 b = 12 - c và a - 1 2 + b - 1 2 + c - 1 2 = 2 . Tổng a + b + c bằng?
A. 3
B. 2
C. 1
D. 0
Cho 4 số a, b, c, d thỏa mãn
0
a
b
1
c
d
.
Số lớn nhất trong 4 số
log
a
b
,
log
b
c
,
log
c
d
,
log
d...
Đọc tiếp
Cho 4 số a, b, c, d thỏa mãn 0 < a < b < 1 < c < d . Số lớn nhất trong 4 số log a b , log b c , log c d , log d a là:
A. log a b .
B. log b c .
C. log c d .
D. log d a .
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn
a
−
3
2
+
b
−
6
2
1
v
à
4
c
+
3
d
−
5
0
. Tính giá trị nhỏ nhất của
T...
Đọc tiếp
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn a − 3 2 + b − 6 2 = 1 v à 4 c + 3 d − 5 = 0 . Tính giá trị nhỏ nhất của T = c − a 2 + d − b 2
A. 16
B. 18
C. 9
D. 15
Cho
a
,
b
0
,
a
≠
1
thỏa mãn
log
a
b
b
4
log
2
a
16
b
Tổng a+b bằng A. 16 B. 17 C. 18 D. 19
Đọc tiếp
Cho a , b > 0 , a ≠ 1 thỏa mãn log a b = b 4 log 2 a = 16 b Tổng a+b bằng
A. 16
B. 17
C. 18
D. 19