Gọi M a ; b ; N c ; d
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
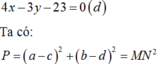
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có

Khi đó

Chọn D.
Gọi M a ; b ; N c ; d
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
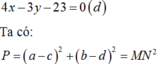
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có

Khi đó

Chọn D.
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn a − 3 2 + b − 6 2 = 1 v à 4 c + 3 d − 5 = 0 . Tính giá trị nhỏ nhất của T = c − a 2 + d − b 2
A. 16
B. 18
C. 9
D. 15
Cho các số thực x,y thay đổi thỏa mãn log 2 sinx + 2 cosx + 2 = 2 cosx - sinx + 3 . Gọi - a b với a ∈ N * , b ∈ N * , a b tối giản là giá trị nhỏ nhất của biểu thức P= 3 cos 3 x + sin 2 x - 5 cosx . Tính T=a+b.
A.T=200.
B. T=257.
C. T=210.
D. T=240
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3 a = 5 b = 15 - c . Tìm giá trị nhỏ nhất của biểu thức P = a 2 + b 2 + c 2 - 4 a + b + c
A. - 3 - log 5 3
B. -4
C. - 2 - 3
D. - 2 - log 5 3
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405
Cho a, b, c là các số thực dương khác 1 thỏa log a 2 b + log b 2 c = log a c b - 2 log b c b - 3
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = log a b - log b c Giá trị của biểu thức S = 2 m + 3 M bằng
A. S = 1 3
B. S = 2 3
C. S = 2
D. S = 3
15.
Cho a, b, c là các số thực dương thỏa mãn \(a+b+c+ab+bc+ac=6\)
Chứng minh rằng: \(\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge3\)
16.
Xét các số thực a, b, c ( a khác 0) sao cho:
Phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm m, n thỏa mãn: \(0\le m\le1;0\le n\le1\).
Tìm giá trị nhỏ nhất của biểu thức: \(Q=\dfrac{2a^2-ac-2ab+bc}{a^2-ab+ac}\)
17.
Cho ba số thực không âm a, b, c và thỏa amnx a+b+c=1.
Chứng minh rằng: \(a+2b+c\ge4\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
18.
Cho ba số thực a, b, c. Chứng minh rằng:
\(\left(a^2-bc\right)^3+\left(b^2-ca\right)^3+\left(c^2-ab\right)^3\ge3\left(a^2-bc\right)\left(b^2-ca\right)\left(c^2-ab\right)\)
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho số phức z = a + bi ( a , b ∈ ℕ ) thỏa mãn đồng thời hai điều kiện | z | = | z - 1 - i | và biểu thức A = | z - 2 + 2 i | + | z - 3 + i | đạt giá trị nhỏ nhất. Giá trị của biểu thức a + b bằng
A. -1.
B. 2.
C. -2.
D. 1.