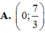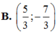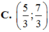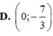\(T=\left(x_A-2y_A+2\right)\left(x_B-2y_B+2\right)=60>0\)
=> A và B nằm cùng phía so với d
a)Lấy B' đối xứng với B qua d
=> d là trung trực của BB'
Có \(MA+MB=MA+MB'\)
Để MA+MB nn <=> MA+MB' nhỏ nhất <=> M;A;B' thẳng hàng <=> \(\overrightarrow{AM};\overrightarrow{AB'}\) cùng phương
\(BB'\left\{{}\begin{matrix}quaB\left(2;5\right)\\\perp d\Rightarrow vtcp\overrightarrow{n}\left(2;1\right)\end{matrix}\right.\)
\(\Rightarrow BB':2x+y-9=0\)
Gọi \(F=BB'\cap d\) \(\Rightarrow F\left(\dfrac{16}{5};\dfrac{13}{5}\right)\)
F là trung điểm của BB' \(\Rightarrow B'\left(\dfrac{22}{5};\dfrac{1}{5}\right)\)
\(M\in\left(d\right)\Rightarrow M\left(2t-2;t\right)\)
\(\Rightarrow\overrightarrow{AB'}\left(\dfrac{22}{5};-\dfrac{29}{5}\right)\);\(\overrightarrow{AM}\left(2t-2;t-6\right)\)
\(\overrightarrow{AM};\overrightarrow{AB'}\) cp <=> \(\dfrac{22}{5}\left(t-6\right)=-\dfrac{29}{5}\left(2t-2\right)\)
<=>\(t=\dfrac{19}{8}\)
Vậy \(M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
b) Có \(MA-MB\le AB\)
\(\Leftrightarrow\left|MA-MB\right|\le AB\)
\(\left|MA-MB\right|\) lớn nhất <=> M;A;B thẳng hàng <=> \(\overrightarrow{AM};\overrightarrow{AB}\) cp
\(M\in\left(2t-2;t\right)\)
\(\Rightarrow\overrightarrow{AM}\left(2t-2;t-6\right)\); \(\overrightarrow{AB}\left(2;-1\right)\)
\(\overrightarrow{AM};\overrightarrow{AB}\) cp <=> \(-1\left(2t-2\right)=2\left(t-6\right)\)
\(\Leftrightarrow t=\dfrac{7}{2}\)
\(\Rightarrow\) \(M\left(5;\dfrac{7}{2}\right)\)