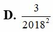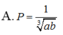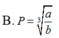Các câu hỏi tương tự
Cho các số thực dương a và b. Rút gọn biểu thức
P
a
-
b
a
4
-
b
4
-
a
+
a
b
4...
Đọc tiếp
Cho các số thực dương a và b. Rút gọn biểu thức P = a - b a 4 - b 4 - a + a b 4 a 4 + b 4 được kết quả là:
A. a 4 - b 4
B. b 4
C. b - a
D. a 4
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Cho hai số thực dương a; b thỏa mãn log2(a + 1) + log2(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là
A.12
B.14
C. 8
D.16
Cho số thực dương a, b. Rút gọn biểu thức
a
3
+
b
3
a
2
3
+
b
2
3
-
a...
Đọc tiếp
Cho số thực dương a, b. Rút gọn biểu thức a 3 + b 3 a 2 3 + b 2 3 - a b 3
A. a 1 3 - b 1 3
B. a - b
C. a + b
D. a 1 3 + b 1 3
Rút gọn biểu thức
P
(
a
π
+
b
π
)
-
(
4
1...
Đọc tiếp
Rút gọn biểu thức P = ( a π + b π ) - ( 4 1 π a b ) π với a, b là các số dương.
A.![]()
B. ![]()
C. ![]()
D. ![]()
có bao nhiêu số thực dương a,b sao cho ab+1≤b. Biểu thức P=\(\dfrac{a+b}{\sqrt{a^2}-ab+3b^2}+\dfrac{2a-b}{6\left(a+b\right)}\) đạt giá trị lớn nhất.
Xét phương trình ax3- x2+ bx-10 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2
-
3
a
b
+
2
a
2
(
b
-...
Đọc tiếp
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Cho a, b là các số thực dương, khác 1. Đặt
log
a
b
α
Biểu thức
P
log
a
2
b
-
log
b
a
3
là:
Đọc tiếp
Cho a, b là các số thực dương, khác 1. Đặt log a b = α Biểu thức P = log a 2 b - log b a 3 là:
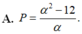
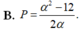
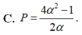

Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Đọc tiếp
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
![]()
![]()
![]()