Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
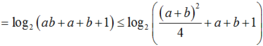
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
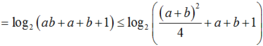
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Cho hai số thực dương a, b thỏa mãn hệ thức: 2 log 2 a - log 2 b ≤ log 2 a + 6 b . Tìm giá trị lớn nhất P m a x của biểu thức P = a b - b 2 a 2 - a b + 2 b 2
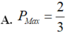
![]()
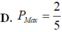
Cho hai số dương x, y thỏa mãn l o g 2 ( 4 x + y + 2 x y + 2 ) y + 2 = 8 - 2 x - 2 y + 2 . Giá trị nhỏ nhất của P = 2 x + y là số có dạng M = a b + c với a , b ∈ ℕ , a > 2 . Tính S = a + b + c
A. 17
B. 7
C. 19
D. 3
Cho các số thực x,y dương thỏa mãn log 2 x + 2 y 2 = log 2 x + 4 log 4 y . Giá trị nhỏ nhất của biểu thức P = x 2 1 + 4 y + y 2 2 x + 1
A. 4.
B. 32 9 .
C. 37 9 .
D. 10 3 .
Cho các số thực x,y thay đổi thỏa mãn log 2 sin x + 2 cos x + 2 = 2 cos x - sin x + 3 . Gọi - a b với a , b ∈ ℕ * , a b tối giản là giá trị nhỏ nhất của biểu thức P = 3 cos 3 x + sin 2 x - 5 cos x Tính T = a +b
A. T = 200
B. T = 257
C. T = 210
D. T = 240
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Xét các số thực a, b thỏa mãn 1 4 < b < a < 1 Biểu thức P = log a ( b - 1 4 ) - log a b b đạt giá trị nhỏ nhất khi
A. log a b = 1 3
B. log a b = 2 3
C. log a b = 3 2
D. log a b = 3
cho ba số thực dương a b c thỏa mãn ab+bc+ac≤1. tìm giá trị nhỏ nhất của biểu thức P biết:
P= \(\dfrac{1}{\sqrt{a^2+b^2-abc}}+\dfrac{1}{\sqrt{a^2+c^2-abc}}+\dfrac{1}{\sqrt{c^2+b^2-abc}}\)
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Cho a, b là hai số thực dương và a ≠ 1 thỏa mãn log a b = 2 Tính giá trị biểu thức P = log a 2 b b 2 a
A. P = 2 + 3 2 2
B. P = 2 2 2 + 1
C. P = 2 - 1 2 + 1
D. P = - 6 + 5 2 2