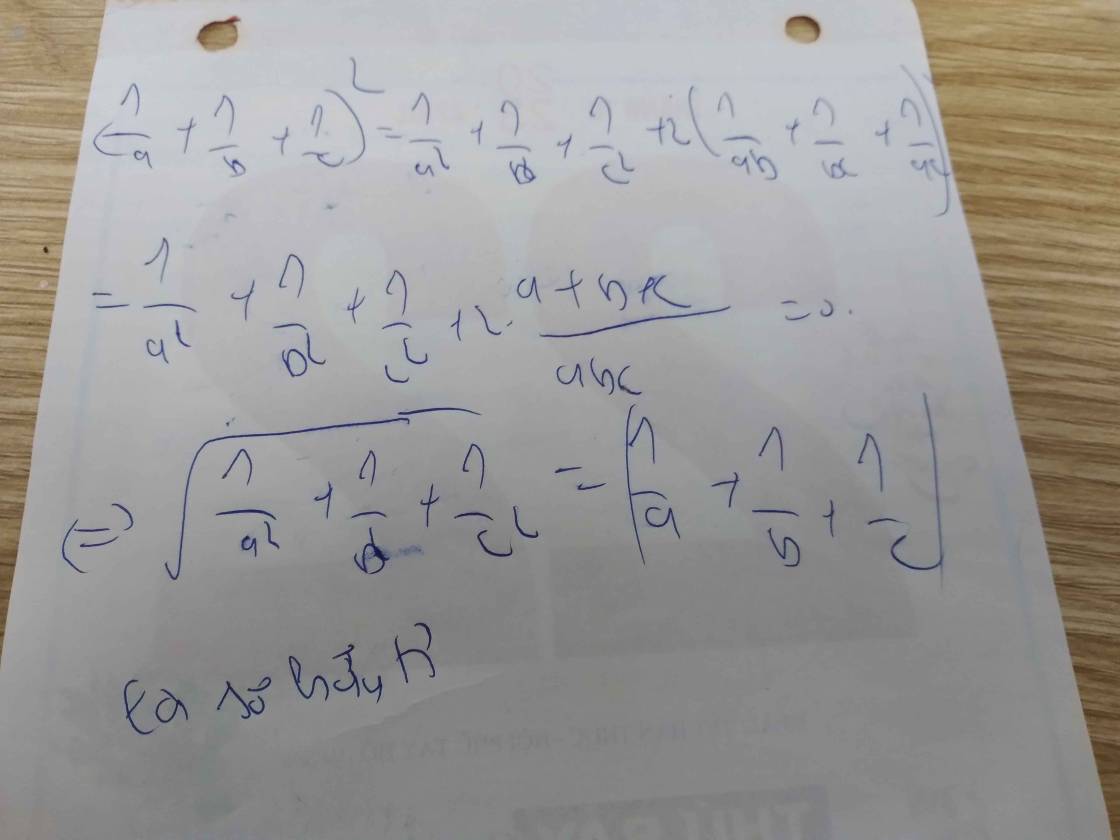Question

Cho a, b, c \(\ne0\) và a+b+c=0. CMR :

\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)  là số hữu tỉ

Answer 1

Ta có: \(2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)=\dfrac{2\left(a+b+c\right)}{abc}=0\)

\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)}\)

\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\left|\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right|\) là số hữu tỉ

Answer 2