Các câu hỏi tương tự
Cho A(4; 0; 0),
B
0
;
0
;
m
2
+
3
m
∈
ℝ
. Điểm H di động trên đường thẳng AB. Xác định m để đoạn OH ngắn nhất bằng
12
5
.
Đọc tiếp
Cho A(4; 0; 0), B 0 ; 0 ; m 2 + 3 m ∈ ℝ . Điểm H di động trên đường thẳng AB. Xác định m để đoạn OH ngắn nhất bằng 12 5 .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A(1;2;-3) mặt phẳng (P): 2x+2y-z+90 và đường thẳng
∆
:
x
+
1
3
y
4
z
+
2
-
4
Đường thẳng d đi qua A, song song với
∆
và cắt tại B. Điểm M di động trên (P) sao c...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;2;-3) mặt phẳng (P): 2x+2y-z+9=0 và đường thẳng ∆ : x + 1 3 = y 4 = z + 2 - 4 Đường thẳng d đi qua A, song song với ∆ và cắt tại B. Điểm M di động trên (P) sao cho tam giác AMB luôn vuông tại M. Độ dài đoạn MB có giá trị lớn nhất bằng
![]()
![]()
![]()
![]()
Cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
+
1
2
4...
Đọc tiếp
Cho mặt cầu S : x - 1 2 + y - 2 2 + z + 1 2 = 4 và mặt phẳng P : 2 x + 2 y - z + 2 = 0 . Điểm M di động trên (S), N di động trên (P). Tìm độ dài ngắn nhất của đoạn MN
![]()
![]()
![]()
![]()
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)CH 3. Trong không gian Oxyz cho 2 vectơ a (1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8CH 4.Trong không...
Đọc tiếp
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Cho điểm
A
1
;
0
;
0
và mặt phẳng
P
:
y
+
z
-
3
0
. Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
Đọc tiếp
Cho điểm A 1 ; 0 ; 0 và mặt phẳng P : y + z - 3 = 0 . Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
![]()
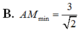
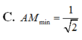
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1 ;2 ;-3) và mặt phẳng
P
:
2
x
+
2
y
-
z
+
9
0
. Đường thẳng d đi qua A và có véctơ chỉ phương
u
→
(
3
;
4
;
-
4
)
cắt (P) tại B. Điểm M thay đổi trong (P) sao...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1 ;2 ;-3) và mặt phẳng P : 2 x + 2 y - z + 9 = 0 . Đường thẳng d đi qua A và có véctơ chỉ phương u → ( 3 ; 4 ; - 4 ) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc 90 ° . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
A. H(-2;-1;3)
B. I(-1;-2;3)
C. K(3;0;15)
D. J(-3;2;7)
Trong không gian tọa độ oxyz, cho mặt cầu (S): (x-1)^2+(y-2)^2+(z+3)^2=6 và hai điểm B(2;3;-1) và C(0;1;-5). Điểm A thuộc mặt cầu (S) sao cho AB<AC. Tia phân giác trong của góc BAC cắt mặt cầu (S) tại K. Hình chiếu của A trên đường thẳng BC là điểm H(a;b;c). Biết AH/AK= căn 15/17, khi đó a+b+c bằng
Cho đoạn thẳng AB cố định trong không gian và có độ dài AB 2. Qua các điểm A và B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M N, sao cho AM+2BN3. Tìm giá trị lớn nhất của thể tích khối tứ diện ABMN ?
Đọc tiếp
Cho đoạn thẳng AB cố định trong không gian và có độ dài AB = 2. Qua các điểm A và B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M N, sao cho AM+2BN=3. Tìm giá trị lớn nhất của thể tích khối tứ diện ABMN ?


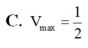
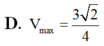
Trong không gian Oxyz cho đường thẳng
△
:
x
-
1
+
2
m
t
y
-
(
m...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng △ : x = - 1 + 2 m t y = - ( m 2 + 1 ) t z = ( 1 - m 2 ) t Gọi △ ' là đường thẳng qua gốc toạ độ O và song song với △ Gọi A,B,C lần lượt là các điểm di động trên Oz, △ , △ ' Giá trị nhỏ nhất của AB+BC+CA bằng
![]()
![]()

![]()





