Question

Cho 2 đường thẳng y= 2x (d1) và y= x + 2 ( d2)
a) Vẽ d1, d2 trên cùng mặt phẳng tọa độ
b) Tìm giao điểm A của d1 và d2
c0 Gọi giao điểm của d2 và Õ là B. Tính Soab?
d) Tìm điểm C để OACB là hình bình hành

Answer 1

a: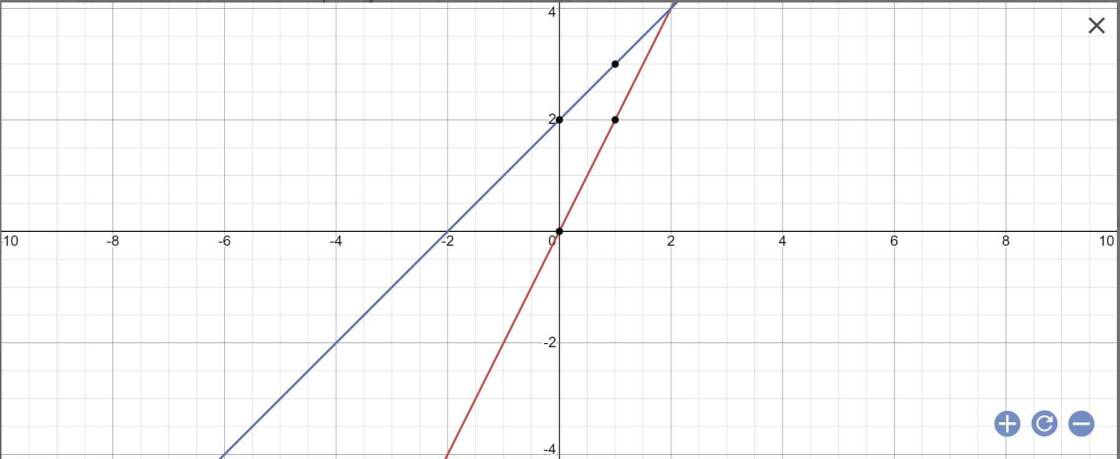 

b: Tọa độ A là:

2x=x+2 và y=2x

=>x=2 và y=4

c: Tọa độ B là:

y=0 và x+2=0

=>x=-2 và y=0

O(0;0); A(2;4); B(-2;0)

\(OB=\sqrt{\left(-2\right)^2+0^2}=2\)

\(OA=\sqrt{2^2+4^2}=2\sqrt{5}\)

\(AB=\sqrt{\left(-2-2\right)^2+4^2}=4\sqrt{2}\)

\(cosOAB=\dfrac{AO^2+AB^2-OB^2}{2\cdot AO\cdot AB}=\dfrac{3\sqrt{10}}{10}\)

=>sin OAB=1/căn 10

\(S_{OAB}=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{10}}\cdot2\sqrt{5}\cdot4\sqrt{2}=4\)