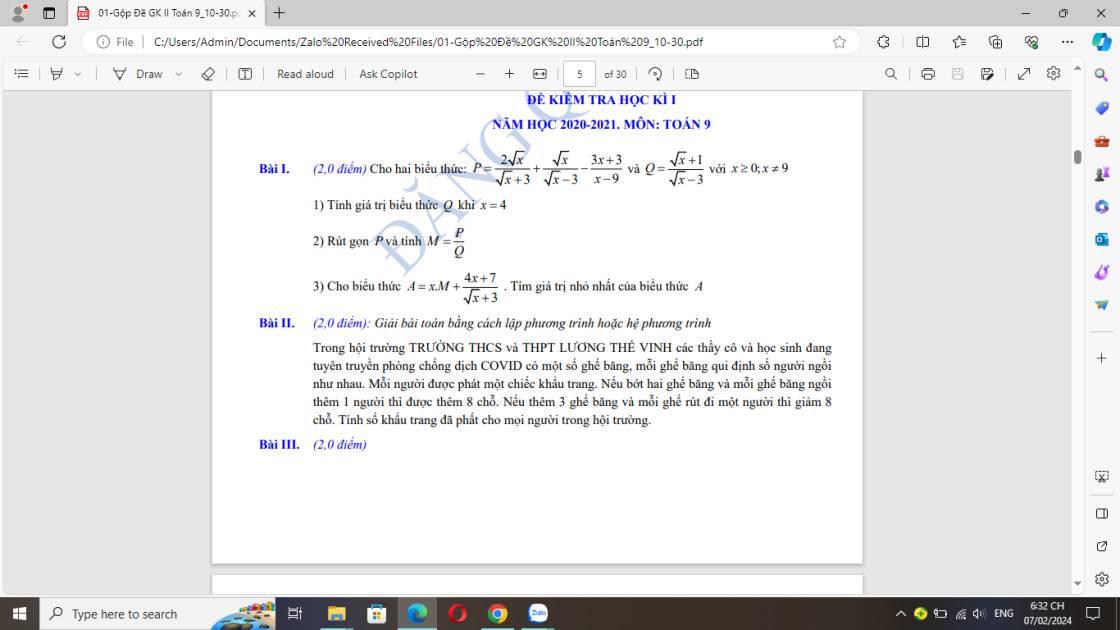
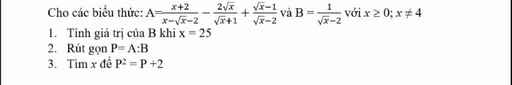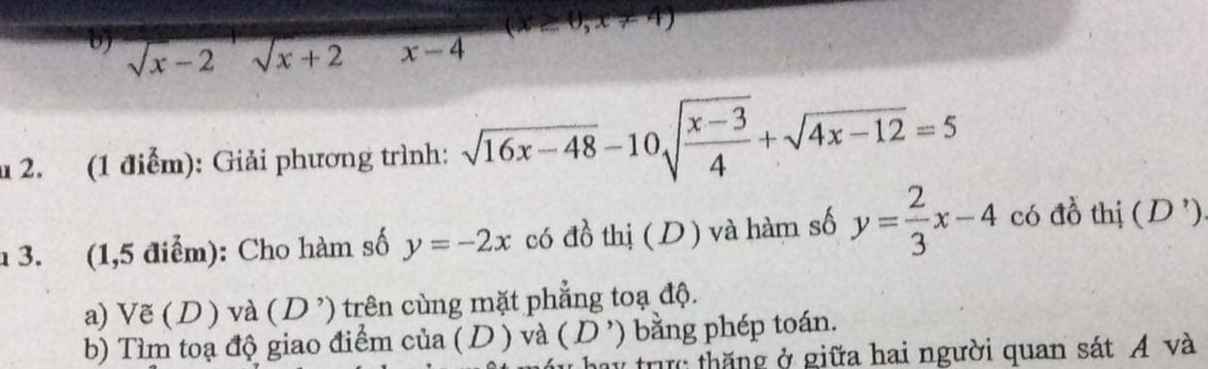Bài 1:
1) Thay `x=4` vào Q ta có:
\(Q=\dfrac{\sqrt{4}+1}{\sqrt{4}-3}=\dfrac{2+1}{2-3}=-3\)
2) \(P=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{P}{Q}\)
\(=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)\cdot\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3}{\sqrt{x}+3}\)
3) \(A=x\cdot M+\dfrac{4x+7}{\sqrt{x}+3}\)
\(A=x\cdot\dfrac{-3}{\sqrt{x}+3}+\dfrac{4x+7}{\sqrt{x}+3}\)
\(A=\dfrac{-3x+4x+7}{\sqrt{x}+3}\)
\(A=\dfrac{x+7}{\sqrt{x}+3}\)
\(A=\dfrac{x-9}{\sqrt{x}+3}+\dfrac{16}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{16}{\sqrt{x}+3}=\sqrt{x}+3+\dfrac{16}{\sqrt{x}+3}-6\)
Áp dụng BĐT cô-si ta có:
\(A=\sqrt{x}+3+\dfrac{16}{\sqrt{x}+3}-6\ge2\sqrt{\left(\sqrt{x}+3\right)\cdot\dfrac{16}{\sqrt{x}+3}}-6=2\sqrt{16}-6=2\)
Dấu "=" xảy ra:
\(\sqrt{x}+3=\dfrac{16}{\sqrt{x}+3}\Leftrightarrow\left(\sqrt{x}+3\right)^2=16\)
\(\Leftrightarrow\sqrt{x}+3=4\Leftrightarrow x=1\)
Vậy: ...
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
