Bảng xét dấu:
| x | 0 | 1 | 2 |
| \(y=3x\) | 0 | 3 | 6 |
| y=3x+4 | 4 | 7 | 10 |
| \(y=-\dfrac{1}{2}x+3\) | 3 | 5/2 | 2 |
| \(y=-\dfrac{1}{2}x\) | 0 | -1/2 | -1 |
vẽ đồ thị:
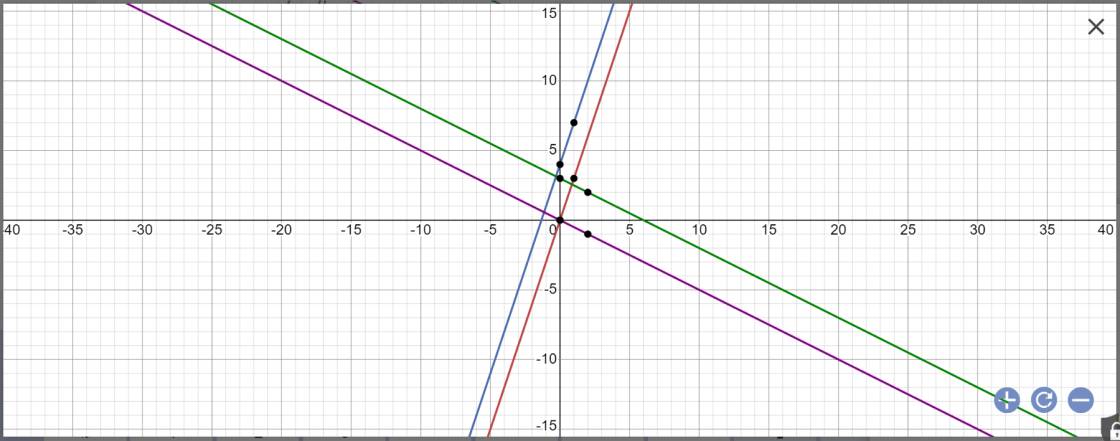
Để vẽ các đường thẳng y = 3x, y = 3x + 4, y = -1/2x + 3 và y = -1/2x trên mặt phẳng tọa độ, chúng ta sẽ sử dụng hệ số góc và điểm cắt trục y của mỗi đường thẳng.
Đường thẳng y = 3x có hệ số góc là 3 và điểm cắt trục y là (0,0). Ta có thể vẽ đường thẳng này bằng cách bắt đầu từ điểm (0,0) và dùng hệ số góc 3 để vẽ đường thẳng đi qua các điểm khác trên mặt phẳng.
Đường thẳng y = 3x + 4 có hệ số góc là 3 và điểm cắt trục y là (0,4). Ta có thể vẽ đường thẳng này bằng cách bắt đầu từ điểm (0,4) và dùng hệ số góc 3 để vẽ đường thẳng đi qua các điểm khác trên mặt phẳng.
Đường thẳng y = -1/2x + 3 có hệ số góc là -1/2 và điểm cắt trục y là (0,3). Ta có thể vẽ đường thẳng này bằng cách bắt đầu từ điểm (0,3) và dùng hệ số góc -1/2 để vẽ đường thẳng đi qua các điểm khác trên mặt phẳng.
Đường thẳng y = -1/2x không có điểm cắt trục y, nên ta có thể vẽ đường thẳng này bằng cách bắt đầu từ điểm (0,0) và dùng hệ số góc -1/2 để vẽ đường thẳng đi qua các điểm khác trên mặt phẳng.
Dưới đây là hình vẽ các đường thẳng trên mặt phẳng tọa độ:
```
| /
| /
| /
| /
| /
| /
| /
|/
---+-----------------
```
Đường thẳng y = 3x được biểu diễn bởi đường thẳng có góc nghiêng dương và đi qua gốc tọa độ (0,0).
Đường thẳng y = 3x + 4 được biểu diễn bởi đường thẳng có góc nghiêng dương và đi qua điểm (0,4) trên trục y.
Đường thẳng y = -1/2x + 3 được biểu diễn bởi đường thẳng có góc nghiêng âm và đi qua điểm (0,3) trên trục y.
Đường thẳng y = -1/2x được biểu diễn bởi đường thẳng có góc nghiêng âm và đi qua gốc tọa độ (0,0).











