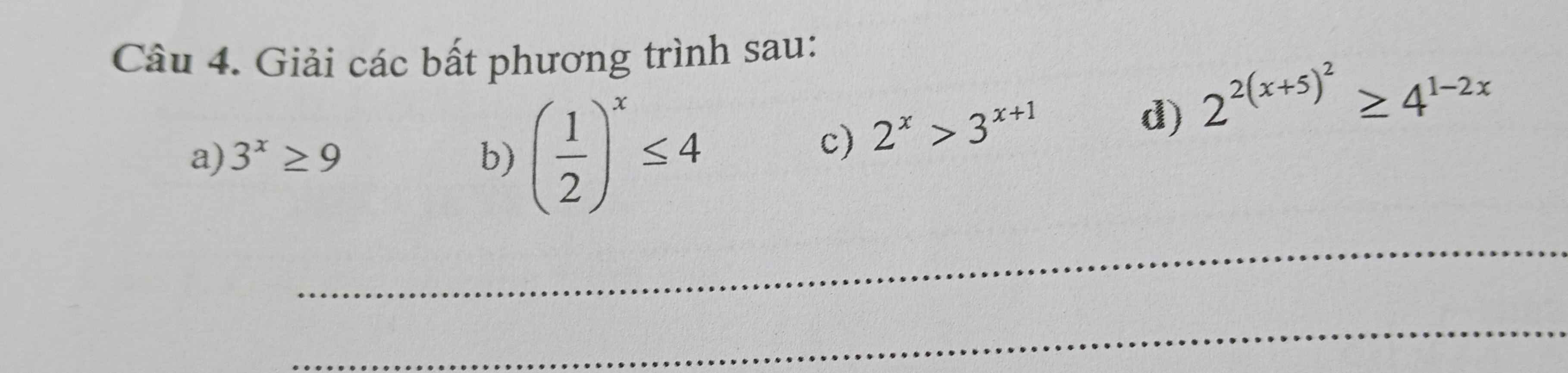a: \(3^x>=9\)
=>\(3^x>=3^2\)
=>x>=2
b: \(\left(\dfrac{1}{2}\right)^x< =4\)
=>\(2^{-x}< =2^2\)
=>-x<=2
=>x>=-2
c: \(2^x>3^{x+1}\)
=>\(log_22^x>log_23^{x+1}\)
=>\(x>\left(x+1\right)\cdot log_23\)
=>\(x-x\cdot log_23>log_23\)
=>\(x\left(1-log_23\right)>log_23\)
=>\(x>\dfrac{log_23}{1-log_23}\)
d: \(2^{2\left(x+5\right)^2}>=4^{1-2x}\)
=>\(2^{2\left(x+5\right)^2}>=2^{2-4x}\)
=>\(2\left(x+5\right)^2>=2-4x\)
=>\(\left(x+5\right)^2>=-2x+1\)
=>\(x^2+10x+25+2x-1>=0\)
=>\(x^2+12x+24>=0\)
=>\(\left(x+6\right)^2>=12\)
=>\(\left[{}\begin{matrix}x+6>=2\sqrt{3}\\x+6< =-2\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>=2\sqrt{3}-6\\x< =-2\sqrt{3}-6\end{matrix}\right.\)