.
\(P=\left(\frac{2x+1}{\sqrt{x^3}-1}-\frac{\sqrt{x}}{x+\sqrt{x}+1}\right):\left(\frac{3}{\sqrt{x}-1}+\frac{2\sqrt{x}+5}{1-x}\right)\)
\(ĐKXĐ:x\ge0,x\ne1\)
\(P=\frac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\frac{\left(\sqrt{x}+1\right)-\left(2\sqrt{x}+5\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-2}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\)
b, \(x=\frac{8}{3-\sqrt{5}}=\frac{2\left(9-5\right)}{3-\sqrt{5}}=2\left(3+\sqrt{5}\right)\)
\(=5+2\sqrt{5}+1=\left(\sqrt{5}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{5}+1\)
\(\Rightarrow P=\frac{\sqrt{5}+1+1}{\sqrt{5}+1-2}=\frac{\sqrt{5}+2}{\sqrt{5}-1}\)
c, \(P=\frac{\sqrt{x}-2+3}{\sqrt{x}-2}=1+\frac{3}{\sqrt{x}-2}\in N\)\(\Rightarrow\frac{3}{\sqrt{x}-2}\in Z\)
\(\Rightarrow\sqrt{x}-2\inƯ\left(3\right)\)
| \(\sqrt{x}-2\) | \(x\) | \(P\) |
| \(-3\) | ( loại ) | 0 |
| \(-1\) | ( loại ) | -2 |
| \(1\) | 9 | 4 |
| \(3\) | 25 | 2 |
\(\Rightarrow x\in\left\{9;25\right\}\)
Bạn ơi, thay x=25/4 vẫn ra P là số tự nhiên nhá, thiếu kìa
nhận giá trị là số nguyên.
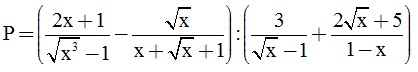
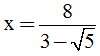và Q = 
(ĐKXĐ: 
)