Câu 2. (2 điểm) Cho hai đa thức
P(x)=5x3 - 3x + 7 - x
Q(x)= -5x3 + 2x - 3 +2x - x2 - 2
a) Thu gọn hai đa thức P(x) và Q(x).
b)Tìm đa thức M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x)
c)Tìm nghiệm của đa thức M(x).
Câu 3: (3,0 điểm).Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE ^ BC (E Î BC). Chứng minh DA = DE.
c) ED cắt AB tại F. Chứng minh DADF = DEDC rồi suy ra DF > DE.
3,
tự vẽ hình
a,
Xét Δ ABC, có :
\(BC^2=5^2=25\left(cm\right)\)
\(AB^2+AC^2=3^2+4^2=9+16=25\left(cm\right)\)
=> \(BC^2=AB^2+AC^2\)
=> Δ ABC vuông tại A (Py - ta - go đảo)
b, c, ?
Câu `2:`
`a)`
`@P(x)=5x^3-3x+7-x`
`=>P(x)=5x^3-(3x+x)+7`
`=>P(x)=5x^3-4x+7`
`@Q(x)=-5x^3+2x-3+2x-x^2-2`
`=>Q(x)=-5x^3-x^2+(2x+2x)-(3+2)`
`=>Q(x)=-5x^3-x^2+4x-5`
_________________________________________________________
`b)`
$\bullet$ `M(x)=P(x)+Q(x)`
`=>M(x)=5x^3-4x+7-5x^3-x^2+4x-5`
`=>M(x)=-x^2+2`
$\bullet$ `N(x)=P(x)-Q(x)`
`=>N(x)=5x^3-4x+7+5x^3+x^2-4x+5`
`=>N(x)=10x^3+x^2-8x+12`
__________________________________________________________
`c)` Cho `M(x)=0`
`=>-x^2+2=0`
`=>x^2=2`
`=>x=+-\sqrt{2}`
\(\text{Bài 2:a)}P\left(x\right)=5x^3-3x+7-x\)
\(P\left(x\right)=5x^3+\left(-3x-x\right)+7\)
\(P\left(x\right)=5x^3-4x+7\)
\(Q\left(x\right)=-5x^3+2x-3+2x-x^2-2\)
\(Q\left(x\right)=-5x^3-x^2+\left(2x+2x\right)+\left(-3-2\right)\)
\(Q\left(x\right)=-5x^3-x^2+4x-5\)
\(\text{b)M(x)=P(x)+Q(x)}\)
\(M\left(x\right)=\left(5x^3-4x+7\right)+\left(-5x^3-x^2+4x-5\right)\)
\(M\left(x\right)=5x^3-4x+7+-5x^3-x^2+4x-5\)
\(M\left(x\right)=\left(5x^3-5x^3\right)-x^2+\left(-4x+4x\right)+\left(7-5\right)\)
\(M\left(x\right)=-x^2+2\)
\(N\left(x\right)=P\left(x\right)-Q\left(x\right)\)
\(N\left(x\right)=\left(5x^3-4x+7\right)-\left(-5x^3-x^2+4x-5\right)\)
\(N\left(x\right)=5x^3-4x+7+5x^3+x^2-4x+5\)
\(N\left(x\right)=\left(5x^3+5x^3\right)+x^2+\left(-4x-4x\right)+\left(7+5\right)\)
\(N\left(x\right)=10x^3+x^2-8x+12\)
\(\text{c)Đặt M(x)=0}\)
\(\Rightarrow-x^2+2=0\)
\(\Rightarrow-x^2\) \(=0-2=-2\)
\(\Rightarrow x^2\) \(=2\)
\(\Rightarrow x\) \(=\pm2\)
\(\text{Vậy đa thức M(x) có 2 nghiệm là }x=-\sqrt{2};x=\sqrt{2}\)
\(\text{Bài 3:}\)
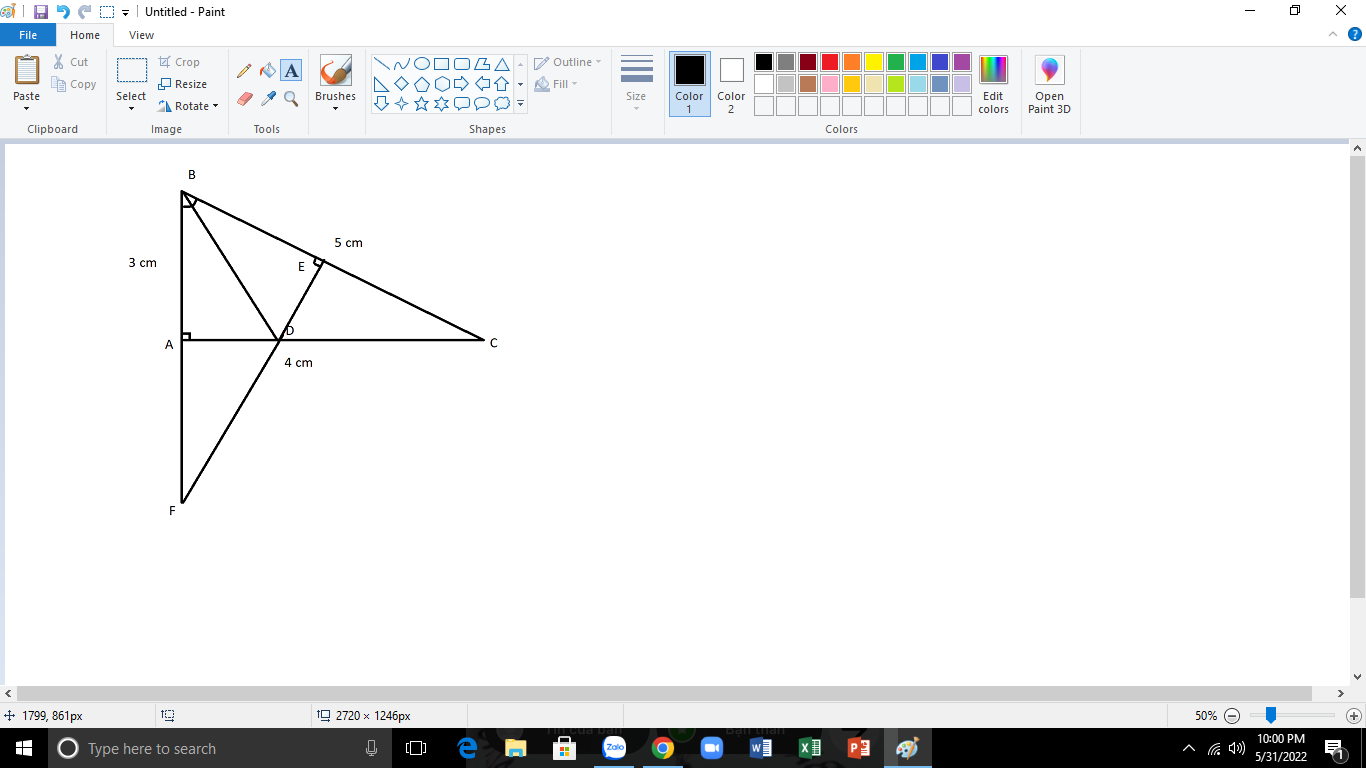
\(\text{a)Ta có:}AB^2+AC^2=3^2+4^2=9+16=25\left(cm\right)\)
\(BC^2=5^2=25\left(cm\right)\)
\(\text{Vì }AB^2+AC^2=BC^2\left(25cm=25cm\right)\)
\(\Rightarrow\Delta ABC\text{ vuông tại A}\)
\(\text{b)Xét }\Delta ABD\text{ và }\Delta EBD\text{ có:}\)
\(BD\text{ chung}\)
\(\widehat{BAD}=\widehat{BED}=90^0\left(gt\right)\)
\(\widehat{ABD}=\widehat{EBD}\left(BD\text{ là phân giác }\widehat{B}\right)\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)\)
\(\Rightarrow DA=DE\left(\text{hai cạnh tương ứng}\right)\)
\(\text{c)Xét }\Delta ADF\text{ và }\Delta EDC\text{ có:}\)
\(DA=DE\left(cmt\right)\)
\(\widehat{ADF}=\widehat{EDC}\left(\text{đối đỉnh}\right)\)
\(\widehat{DAF}=\widehat{DEC}=90^0\left(gt\right)\)
\(\Rightarrow\Delta ADF=\Delta EDC\left(g-c-g\right)\)
\(\text{Xét }\Delta ADF\text{ vuông tại A có:}\)
\(\text{DF là cạnh huyền lớn nhất}\)
\(\Rightarrow DF>DA\)
\(\text{Mà DA=DE(cmt)}\)
\(\Rightarrow DF>DE\)

















