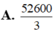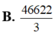Câu 1: Một vật chuyển động theo quy luật S= \(-\dfrac{1}{2}\)t\(^3\) + 3t\(^2\) +1, với t (giây) là khoảng thời gian tình từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 4 giây, kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu?
Câu 2: Tìm phương trình tiệm cận đứng của đồ thị hàm số y = log\(_{2020}\)x.
Câu 1:
\(S=-\frac12t^3+3t^2+1\)
=>\(V\left(t\right)=S^{\prime}\left(t\right)=-\frac12\cdot3t^2+3\cdot2t=-\frac32t^2+6t=-1,5\left(t^2-4t\right)\)
\(=-1,5\left(t^2-4t+4-4\right)=-1,5\left(t-2\right)^2+6\le6\forall t\)
Dấu '=' xảy ra khi t-2=0
=>t=2∈[0;4]
=>Trong khoảng thời gian 4 giây kể từ khi vật bắt đầu chuyển động, vận tốc lớn nhất là 6m/s