Gọi E là giao của AI với BC
F là giao của AJ với BD
Gọi M là giao của EF và BM
Chọn mp(AFE) có chứa IJ
FE cắt BM tại N
nên \(N\in\left(ABM\right)\cap\left(AFE\right)\)
=>(ABM) giao (AFE)=AN
Gọi giao của AN với IJ là K
=>K là giao của JI với (AMB)
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK= 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
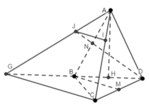
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là:
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của α với BD và AD. Xét các mệnh đề sau:
(1) MP // BC
(2) MQ // AC
(3) PQ // AI
(4) (MPQ) // (ABC)
Số mệnh đề đúng là:
Gọi M, N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MầM NON và P là 1 điểm bất kỳ trong không gian. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ I A → + ( 2 k - 1 ) I B → + k I C → + I D → = 0 → ?
A. k = 2
B. k = 4
C. k = 1
D. k = 0
Cho tứ điện ABCD , gọi I, J, K lần lượt là trung điểm của AC, BC, BD Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
A. Đường thẳng qua J song song với AC
B. Đường thẳng qua I song song với AD
C. Đường thẳng qua K song song với AB
D. Đường thẳng qua J song song với CD
Cho tứ diện ABCD . Gọi E, F lần lượt là trung điểm của AB và CD, I là trung điểm của ED. Khẳng định nào sau đây là khẳng định sai?
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ M N → = k ( A D → + B C → ) ?
A. k = 3
B. k = 1 2
C. k = 2
D. k = 1 3
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ M N → = k ( A D → + B C → )
A. k = 3
B. k = 1 2
C. k = 2
D. k = 7 5
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a3
C. a 3 12
D. a 3 24
