Đáp án A.
Hướng dẫn giải: Dễ dàng ta có được
![]()
Đáp án A.
Hướng dẫn giải: Dễ dàng ta có được
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB//CD). Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
![]()
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây sai?
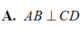
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác cân ABC cân tại C. Gọi I là trung điểm của AB. Biết SA=SB và (SAB) ⊥ (ABC). Khẳng định nào sau đây là sai?
A. SI ⊥ (SAB).
B. IC ⊥ (SAB)
C. (SAC) = (SBC)
D. SC ⊥ (SAB)
Cho hình tứ diện ABCD, lấy M là điểm tùy ý trên cạnh AD (M khác A,D). Gọi (P) là mặt phẳng đi qua M song song với mặt phẳng (ABC) lần lượt cắt DB, DC tại N, P. Khẳng định nào sau đây sai?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD và điểm G thỏa mãn G A → + G B → + G C → + G D → = 0 → (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ B C D . Trong các khẳng định sau, khẳng định nào đúng
A. G A → = − 3 G A G →
B. G A → = 4 G A G →
C. G A → = 3 G A G →
D. G A → = 2 G A G →
Cho hình chóp S.ABCD, O là giao điểm của AC và BD. Gọi M, N, P lần lượt là các điểm thuộc cạnh SA, SB, SD. I là giao điểm của NP và SO. Biết S C ∩ ( M N P ) = Q Khẳng định nào sau đây là sai?
A. I=MD ∩ SO
B. I= MQ ∩ SO
C. I=SO ∩ (MNP)
D. I=MQ ∩ NP
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK= 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
![]()
![]()
![]()
![]()