Các câu hỏi tương tự
Cho lăng trụ tam giác ABC.ABC. Đặt
A
A
→
a
→
,
A
B
→
b
→
,
A
C
→
c...
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C'. Đặt A A ' → = a → , A B → = b → , A C → = c → . Gọi I là điểm thuộc CC' sao cho C ' I → = 1 3 C ' C → , điểm G thỏa mãn G B → + G A ' → + G B ' → + G C ' → = 0 → . Biểu diễn véc tơ I G → qua véc tơ a → , b → , c → . Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
A. I G → = 1 4 1 3 a → + 2 b → - 3 c →
B. I G → = 1 3 1 3 a → + b → + 2 c →
C. I G → = 1 4 a → + b → - 2 c →
D. I G → = 1 4 a → + 1 3 b → - 2 c →
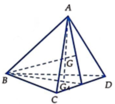
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄. A.
2
4
B.
2
18
C.
9
2
32
D.
2
12
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄.
A. 2 4
B. 2 18
C. 9 2 32
D. 2 12
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt
x
→
A
B
→
,
y
→
A
C
→
,
z...
Đọc tiếp
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt x → = A B → , y → = A C → , z → = A D → . Khẳng định nào sau đây là khẳng định đúng?
A. A G → = 1 3 ( x → + y → + z → )
B. A G → = - 1 3 ( x → + y → + z → )
C. A G → = 2 3 ( x → + y → + z → )
D. A G → = - 2 3 ( x → + y → + z → )
Trong không gian Oxyz, cho tứ diện ABCD có
A
(
1
;
0
;
2
)
,
B
(
-
2
;
1
;
3
)
,
C
(
3
;
2
;
4
)
,
D
(
6
;
9
;
-
5
)
.
Tìm tọa độ trọng tâm G của...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Trong không gian Oxyz, cho tứ diện ABCD có
A
(
1
;
0
;
2
)
,
B
(
-
2
;
1
;
3
)
,
C
(
3
;
2
;
4
)
,
D
(
6
;
9
;
-
5
)
.
Tìm tọa độ trọng tâm G của tứ diện ABCD A.
G
-
9...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A(
x
A
;
y
A
,
z
A
), B(
x
B
;
y
B
,
z
B
), C(
x
C
;
y
C...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A( x A ; y A , z A ), B( x B ; y B , z B ), C( x C ; y C , z C ). Gọi M là trung điểm của BC, G là trọng tâm tam giác ABC. Khẳng định nào sau đây là sai?
A. M x B + x C 2 ; y B + y C 2 ; z B + z C 2
B. AB → = x B - x A ; y B - y A ; z B - z A
C. G x A + x B + x C 3 ; y A + y B + y C 3 ; z A + z B + z C 3
D. AB = ( x B - x A ) 2 ; y B - y A 2 ; ( z B - z A ) 2
Trong không gian với hệ tọa độ Oxyz , cho sáu điểm A(0;1;2), B(2;-1;-2), C(3;1;2) thỏa mãn
A
A
→
+
B
B
→
+
C
C
→
. Gọi G′ là trọng tâm tam giác A′B′C′ thì G′ có tọa độ là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho sáu điểm A(0;1;2), B(2;-1;-2), C(3;1;2) thỏa mãn A A ' → + B B ' → + C C ' → . Gọi G′ là trọng tâm tam giác A′B′C′ thì G′ có tọa độ là
![]()
![]()
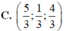
![]()
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
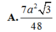
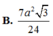
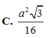
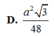
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây? A. Phép tịnh tiến theo vectơ
A
G
→
. B. Phép vị tự tâm A tỉ số
2
3
. C. Phép vị tự tâm M tỉ số
1
3...
Đọc tiếp
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ A G → .
B. Phép vị tự tâm A tỉ số 2 3 .
C. Phép vị tự tâm M tỉ số 1 3 .
D. Phép tịnh tiến theo vectơ M G → .