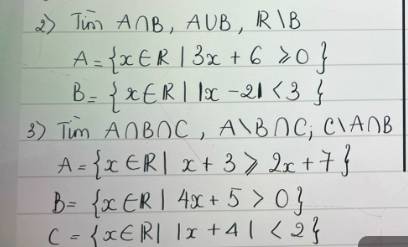cần gấp ạ !


Câu 2. Một mảnh đất hình Elip có độ dài trục lớn bằng \(120m\), độ dài trục bé bằng \(90m\). Tập đoàn VinGroup dự định xây dựng một trung tâm thương mại Vincom trong một hình chữ nhật nội tiếp của Elip như hình vẽ. Tính diện tích xây dựng lớn nhất.
Câu 20: Gọi \(S\) là tập các số tự nhiên có 6 chữ số đôi một khác nhau được lập từ các chữ số \(0; 1; 2; 3; 4; 5; 6; 7; 8\). Chọn ngẫu nhiên một số từ \(S\), tính xác suất để số được chọn không có 2 chữ số chẵn đứng cạnh nhau (kết quả làm tròn đến hàng phần trăm)?
Câu 20 :
Không gian mẫu \(S:n\left(S\right)=8.A^5_8=8.8.7.6.5.4=53760\left(phần.tử\right)\)
\(TH_1:\) \(4\) chữ số lẻ và \(2\) chữ số chẵn
- Sắp xếp \(4\) chữ số lẻ : \(P\left(4\right)=4!=24\left(cách\right)\)
- Đặt 2 chữ số chẵn vào \(5\) vị trí:
+ Không có chữ số \(0\): \(4!.C^2_4.A^2_5=24.6.20=2880\left(cách\right)\)
+ Có chữ số \(0:4!.4.A^2_5-24.4.4=1536\left(cách\right)\)
Tổng trường hợp này là \(2880+1536=4416\left(cách\right)\)
\(TH_2:\) \(3\) chữ số lẻ và \(3\) chữ số chẵn
- Không có chữ số \(0\): \(4!.C^3_4.A^3_4=24.4.24=2304\left(cách\right)\)
- Có chữ số \(0:4!.C^2_4.2A^2_4-A^3_4.C^2_3.A^2_4=24.6.24-24.3.12=2592\left(cách\right)\)
Tổng trường hợp này là \(2304+2592=4896\left(cách\right)\)
Tổng số các số có \(6\) chữ số khác nhau mà không có hai chữ số chẵn nào đứng cạnh nhau là :
\(n\left(A\right)=4416+4896=9312\left(cách\right)\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(S\right)}=\dfrac{9312}{53760}=\dfrac{97}{560}\approx0,17\)