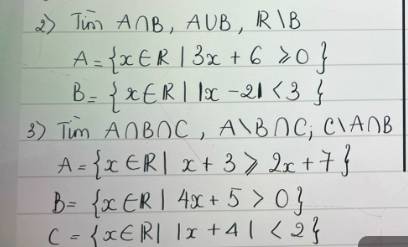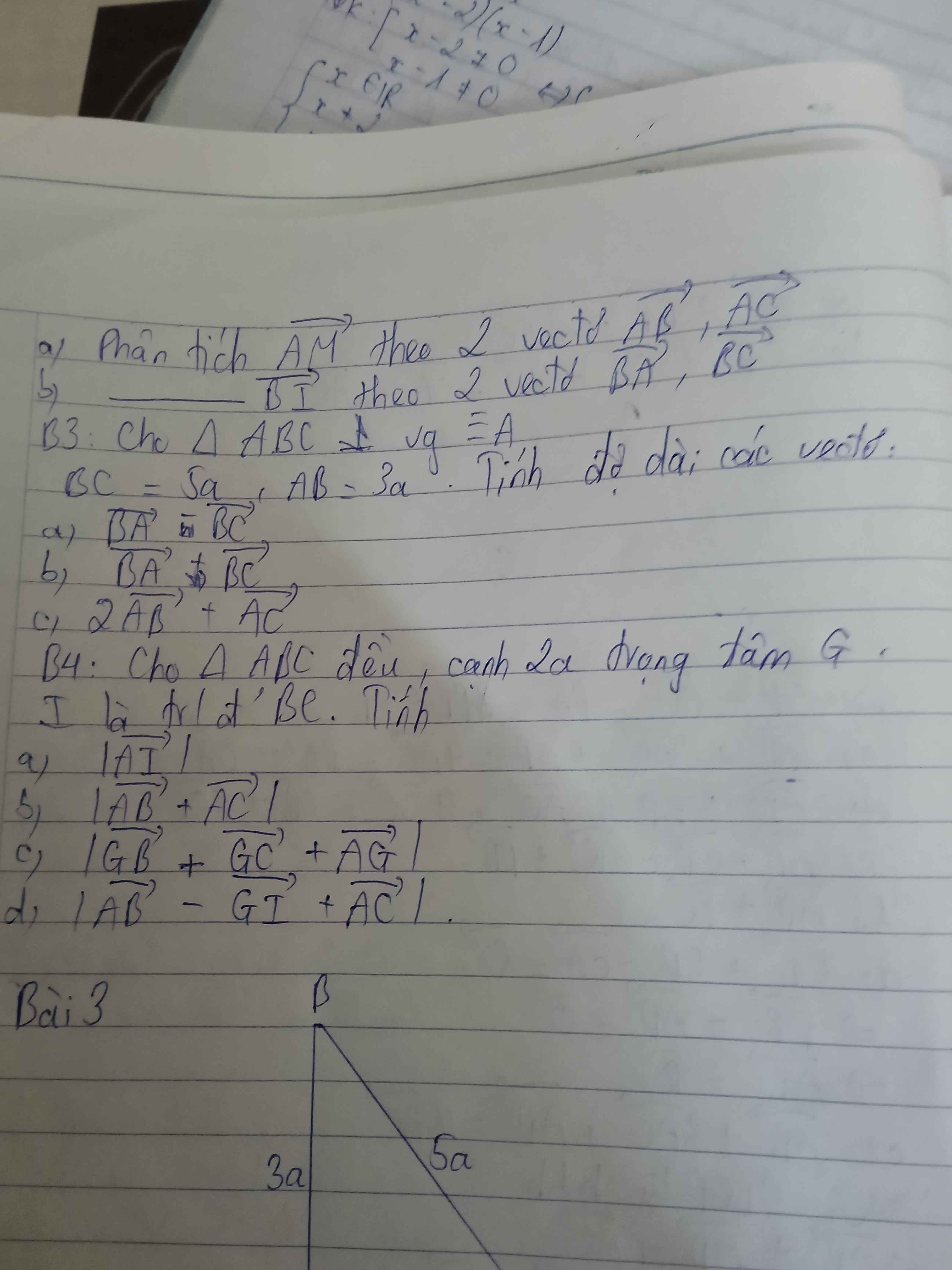Câu 6:
a: Gọi M là trung điểm của BC
\(AM=2a\cdot\dfrac{\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{3}\)
b:
\(AG=GB=GC=\dfrac{2}{3}\cdot a\sqrt{3}=\dfrac{2a\sqrt{3}}{3}\)
\(\left(\overrightarrow{AB}-\overrightarrow{GC}\right)^2=AB^2+GC^2-2\cdot\overrightarrow{AB}\cdot\overrightarrow{GC}\)
\(=4a^2+\dfrac{4}{9}\cdot3\cdot a^2-2\cdot\overrightarrow{GC}\left(\overrightarrow{GB}-\overrightarrow{GA}\right)\)
\(=AB^2+GC^2-2\cdot\overrightarrow{GC}\cdot\left(\overrightarrow{GB}-\overrightarrow{GA}\right)\)
\(=\dfrac{16}{3}a^2-2\cdot\overrightarrow{GC}\cdot\overrightarrow{GB}+2\cdot\overrightarrow{GC}\cdot\overrightarrow{GA}\)
\(=\dfrac{16}{3}a^2-2\cdot GC\cdot GB\cdot cos120+2\cdot GC\cdot GA\cdot cos120\)
=16/3a^2
=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\dfrac{4a}{\sqrt{3}}\)